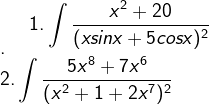indefinite integrals 1

for the second q take x^7 common from denominator then you will get an expression like
(x^-5+x^-7+2)^2*x^14 if you now differentiate this expression you will get the expression of numerator.

\hspace{-16}$Given $\bf{\int\frac{x^2+20}{\left(x\cdot \sin x+\5 \cos x\right)^2}dx}$\\\\\\ Now we can write $\bf{\left(x \cdot \sin x+5\cdot \cos x\right) = \sqrt{x^2+25}\left\{\frac{x}{\sqrt{x^2+25}}\cdot \sin x+\frac{5}{\sqrt{x^2+25}}\cdot \cos x\right\}}$\\\\\\ Now let $\bf{\sin \phi = \frac{x}{\sqrt{x^2+25}}}$ and $\bf{\cos \phi = \frac{5}{\sqrt{x^2+25}}}$ and $\bf{\tan \phi = \frac{x}{5}\Leftrightarrow \phi =\tan^{-1}\left(\frac{x}{5}\right)}$\\\\\\ So $\bf{\left(x \cdot \sin x+5\cdot \cos x\right) = \sqrt{x^2+25}\cdot \cos \left(\phi-x\right)}$\\\\\\ So Integral is $\bf{\int \frac{1}{\cos^2 (\phi-x)}\cdot \left(\frac{x^2+20}{x^2+25}\right)dx = \int \sec^2 \left(\phi-x\right)\cdot \left(\frac{x^2+20}{x^2+25}\right)dx}$\\\\\\ Now let $\bf{\left(\phi-x\right) = \left(\tan^{-1}\left(\frac{x}{5}\right)-x\right)=t\;,}$ Then $\bf{\left(\frac{25}{x^2+25}\cdot \frac{1}{5}-1\right)dx = -\left(\frac{x^2+20}{x^2+25}\right)dx= dt}$\\\\\\

\hspace{-20}$ So $\bf{\left(\frac{x^2+20}{x^2+25}\right)dx = -dt}$\\\\\\ So Integral convert into $\bf{-\int \sec^2 t dt= -\tan (t)+\mathbb{C}}$\\\\\\ $\bf{=-\tan \left(\tan^{-1} \left(\frac{x}{5}\right)-x\right)+\mathbb{C}}$\\\\\\ $\bf{=-\left(\frac{\frac{x}{5}-\tan x}{1+\tan x\cdot \frac{x}{5}}\right)+\mathbb{C}=\left(\frac{5\tan x-x}{x\cdot tan x+5}\right)+\mathbb{C}}$\\\\\\ So $\bf{\int\frac{x^2+20}{\left(x\cdot s\in x+5\cdot \cos x\right)^2}dx = \left(\frac{5\tan x-x}{x\cdot tan x+5}\right)+\mathbb{C}}$

\hspace{-16}$Given $\bf{\int\frac{5x^8+7x^6}{\left(x^2+1+2x^7\right)^2}dx}$\\\\\\ We can write the Integral as ........\\\\\\ $\bf{\int\frac{5x^8+7x^6}{x^{14}\cdot \left(x^{-5}+x^{-7}+2\right)^2}dx = \int\frac{5x^{-6}+7x^{-8}}{\left(x^{-5}+x^{-7}+2\right)^2}dx}$\\\\\\ Now Let $\bf{\left(x^{-5}+x^{-7}+2\right)=t\;,}$ Then $\bf{\left(5x^{-6}+7x^{-8}\right)dx = -dt}$\\\\\\ So Integral Convert into $\bf{-\int\frac{1}{t^2}dt = \frac{1}{t}+\mathbb{C}=\frac{1}{x^{-5}+x^{-7}+2}+\mathbb{C}}$\\\\\\ So $\bf{\int\frac{5x^8+7x^6}{\left(x^2+1+2x^7\right)^2}dx = \left(\frac{x^7}{x^2+1+2x^7}\right)+\mathbb{C}}$