341
man111 singh Nice Solution hsbhatt Sir.Upvote·0· Reply ·2013-10-01 00:49:35
Limn→ ∞ [ n2 . ∫ ( tan-1 nx)/( sin-1 nx) dx
Integration upper limit:- ( 1/n )
Integration lower limit:- { (1+ n ) / n }
-
UP 0 DOWN 0 1 4
4 Answers
341
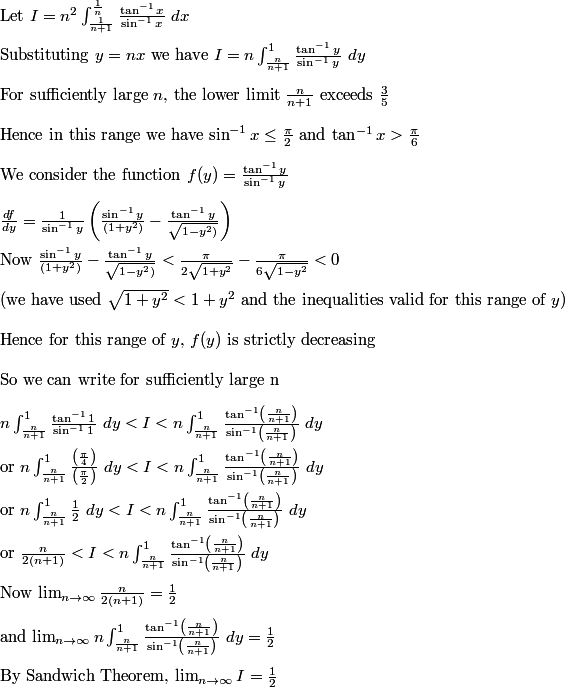
1357Newton-Leibniz might help
Jeet Sen Sharma sir a conceptual question....
while applyin newton lebnitz in dis ques, we will differentiate w.r.t "x" or "n".. ?
1708\hspace{-16}$ Is yours question is $\bf{\lim_{n\rightarrow \infty}n^2 \cdot \int_{\frac{1}{n+1}}^{\frac{1}{n}}\frac{\tan^{-1}(nx)}{\sin^{-1}(nx)}dx}$\\\\\\ Then Answer is $\bf{=\frac{1}{2}}$
