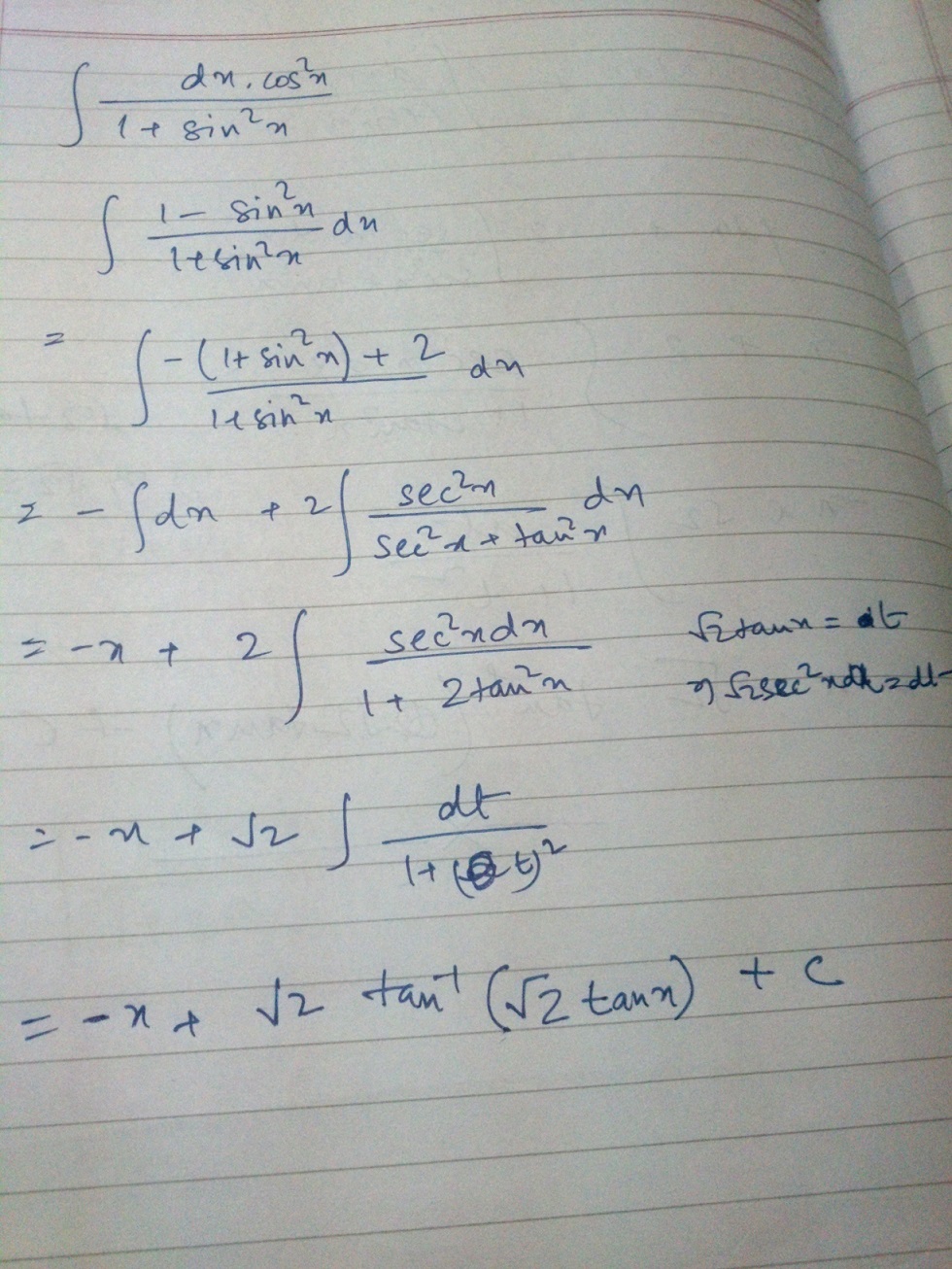
 Manish Shankar yes it is correctUpvote·0· Reply ·2013-09-17 22:47:47
Manish Shankar yes it is correctUpvote·0· Reply ·2013-09-17 22:47:47 Aditya Agarwal Thank You, sir. :)
Aditya Agarwal Thank You, sir. :)
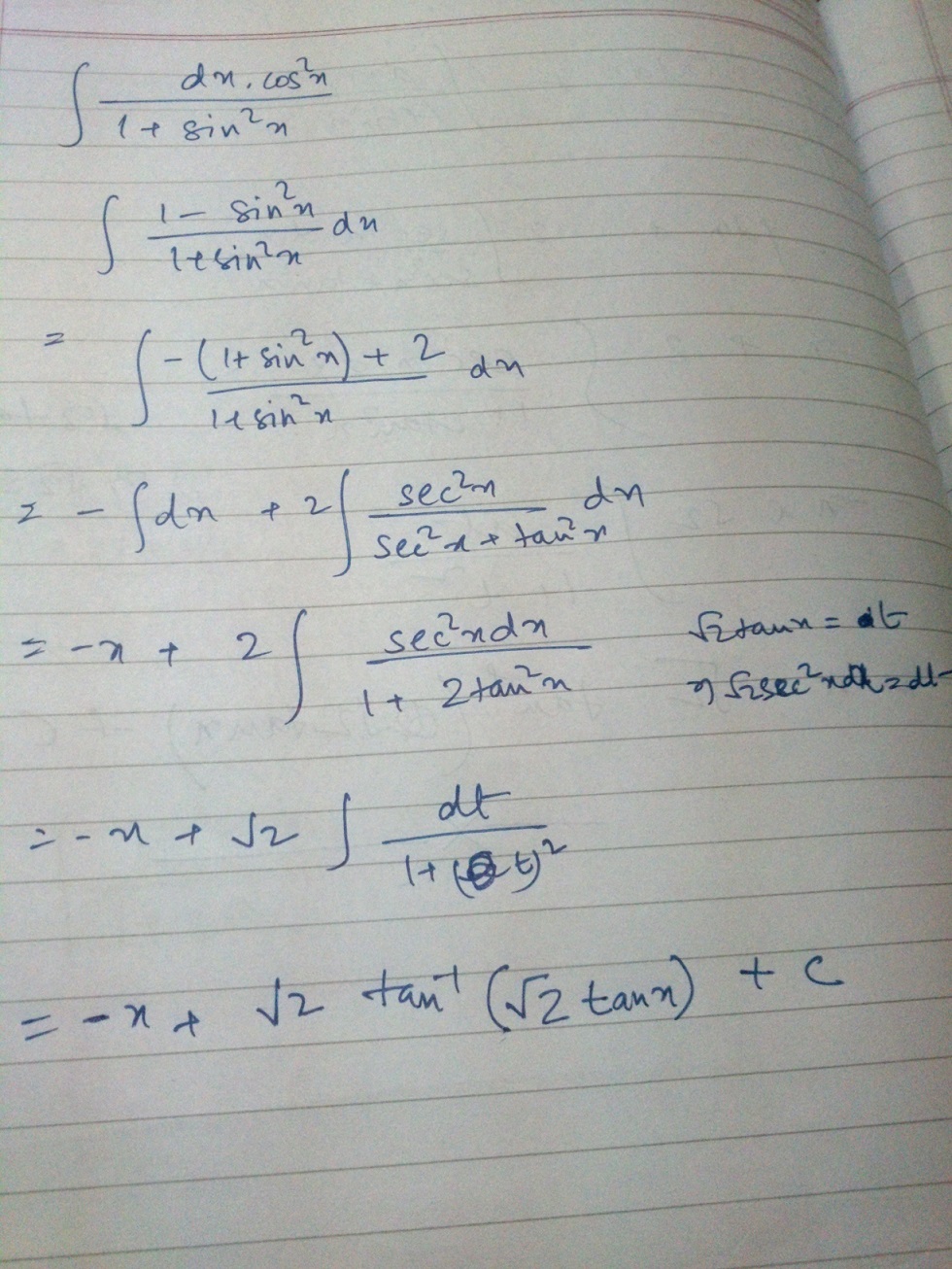
\hspace{-16}\bf{=\int\frac{1}{\sec^2 x+\tan^2 x}dx = \int\frac{1}{1+\tan^2 x+\tan^2 x}dx}$\\\\\\ $\bf{=\int\frac{1}{1+2\tan^2 x}dx}$\\\\\\ Now Let $\bf{\tan x = t\Leftrightarrow dx = \frac{1}{\sec^2 x}dt = \frac{1}{1+t^2}dt}$\\\\\\ $\bf{=\int\frac{1}{(1+t^2).(1+2t^2)}dt}$\\\\\\ $\bf{=\int\frac{2(1+t^2)-(1+2t^2)}{(1+t^2)\cdot (1+2t^2)}dt}$\\\\\\ $\bf{=\int\frac{2}{1+2t^2}dt-\int\frac{1}{1+t^2}dt}$\\\\\\ $\bf{=\int\frac{1}{\left(\frac{1}{\sqrt{2}}\right)^2+t^2}dt-\int\frac{1}{1+t^2}dt}$\\\\\\ $\bf{=\sqrt{2}\cdot \tan^{-1}\left(\sqrt{2}\cdot t\right)-\tan^{-1}(t)+\mathbb{C}}$\\\\\\ $\bf{=\sqrt{2}.\cdot \tan^{-1}\left(\sqrt{2}\cdot \tan x\right)-\tan^{-1}\left(\tan x \right)+\mathbb{C}}$