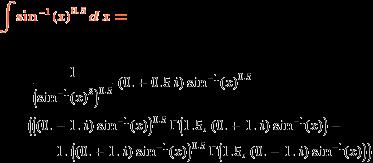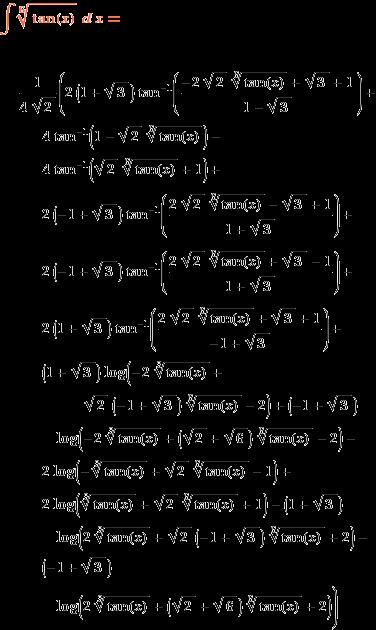got it... it's working..
pls give me hints for the second and third problem
∫(3cosx+2) dx(sinx+2cosx+3)
Please give me a solution to this problem.....
And these too.
∫(tanx)^(1/6)dx
∫√sin^-1(x) dx
it's integration of root under sin inverse x .
-
UP 0 DOWN 0 0 6

6 Answers
for first one
let denominator = f(x)
3cosx+2=Af(x)+Bf'(x)+C=A(sinx+2cosx+3)+B((cosx-2sinx)+C
solving it we get A=6/5, B=3/5, C=-8/5
so the integral becomes
∫(6/5)dx+(3/5)cosx-2sinxsinx+2cosx+3-(8/5)sinx+2cosx+3dx
(6/5)x+(3/5)log(sinx+2cosx+3)-∫(8/5)sinx+2cosx+3dx
for the remaining divide and multiply by cos2x and solve
i think The value of this integral ( example ∫√sinx) is not an elementary function. You can find its value using the Online Integrator.
please check the integration sikho thread by b555
there these type is solved[1]