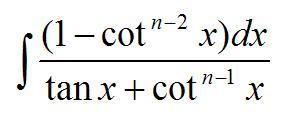Integration

I=\int \frac{1-cot^{n-2}x}{tanx+cot^{n-1}x}dx

let us change this into an expression containing only tan x

I=\int \frac{tan^{n-1}x-tanx}{tan^{n}x+1}dx

=\int \frac{tan^{n-1}x-tanx}{(tan^{n}x+1)(tan^2x+1)}sec^2xdx

Substitute z=tanx

I=\int \frac{z^{n-1}-z}{(z^n+1)(z^2+1)}dz

=\int \frac{z^{n-1}}{z^n+1}dz-\int\frac{z}{z^2+1}dz

=\frac{1}{n}ln(z^n+1)-\frac{1}{2}ln(z^2+1)+C

=\frac{1}{n}ln(tan^nx+1)-\frac{1}{2}ln(tan^2x+1)+C

=ln\left(\frac{(tan^nx+1)^{\frac{1}{n}}}{\sqrt{tan^2x+1}}\right)+C

=\frac{1}{n}ln(sin^nx+cos^nx)+C