1f(x) is an odd function(b)....write the right-hand side expression which is ∫f(x)dx from -2 to +3 as [∫f(x)dx from -2 to +2] + [∫f(x)dx from 2 to 3]....now i think u can solve.... ....
Let f(x) be a continuous function such that f(x) does not vanish for all real values of x if
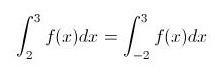then f(x) (for all x ε R) is
(a) an even function
(b) an odd function
(c) a periodic function
(d) None of these
Ans: (d)
-
UP 0 DOWN 0 0 6
6 Answers
1
262debosmit u are right , but it is given that f(x) does not vanish(or f(x)≠0) for all x. but for an odd function, f(0)=0. hence then given function can neither be odd nor be even. hence ans is (D)
1@aditya: 1/x is an odd fnctn but f(0) is not equal to 0....
262oh!! stupid of me ! didnt think of negative powers. yes then it should be (b)
1now i think it should be (d).....f(0) has to be equal to 0 i guess....cant think of any fnctn which satisfies the qstn........
