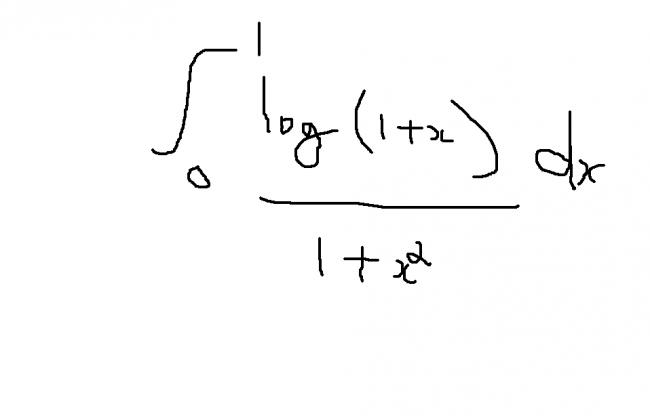1u r right........akand.......gud job........
1coool one dude.......nice substitution.....
1
Terminator
·2009-02-23 08:28:51
Answer :
Let x=tanθ => dx=sec2θ
so integrand changes.....to.........
0∫ π/4 log(1+tanθ).sec2θ.dθ/1+tan2θ
Let I=0∫ π/4 log(1+tanθ).dθ
=0∫ π/4 log(1+ tan(π/4 - θ).dθ
=0∫ π/4 log(1 + 1- tanθ/1+tanθ)dθ
=0∫ π/4 log(2/1+tanθ).dθ
=0∫ π/4 log2 - 0∫ π/4log (1+tanθ).dθ
2I =0∫ π/4 log2
I=Ï€/8 log2
Got it!!!!!!
1
Terminator
·2009-02-23 08:17:00
akand te answer is π/8log2 .......[1][1][1][1][1].....ya der is a mistake....
1
Akand
·2009-02-23 08:13:15
check d second step carefully.......am i rite??? i dunno im confused
1
Akand
·2009-02-23 08:12:28
u sure im rite?????? coz i hav a doubt now
1
Terminator
·2009-02-23 08:11:34
bhaiyya isnt it....????..
1
Terminator
·2009-02-23 08:09:00
but a little bit bigger...[1][1][1][1][1]........
1
Terminator
·2009-02-23 08:06:58
We can do by taking x=tanθ also rite bhaiyya...
1
Terminator
·2009-02-23 07:18:49
reply.........[2][2][2][2][2]..........
1
Akand
·2009-02-23 07:34:09
k ..
use ilate...
we get I= log(1+x)tan-1x-∫tan-1x/(1+x)
= log(1+x)tan-1x+tan-1xlog(1+x)-I
2I=(2log2)∩/4
I=(log2)∩/4
1
Terminator
·2009-02-23 07:31:14
ok.....plz give the solution........
1
Akand
·2009-02-23 07:29:23
k simple w8 i got d solution ...........im typing
1
Terminator
·2009-02-23 07:27:40
no akand itz integrable......
1
Akand
·2009-02-23 07:27:13
cos there is no 'dx'..!!!! hehe just kiddin k im trying dont worry and dont scold me...
1
Akand
·2009-02-23 07:26:23
dude simple............its non integrable........
1
Terminator
·2009-02-23 07:22:54
hey plzz try it yaar.......
