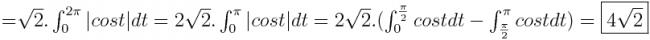1thanxxxxx
i have open this thread to discuss integration questions ... so post questions and we will discuss it...........
-
UP 0 DOWN 0 0 19
19 Answers
11Ans ) I am getting
\ln \left|1 + x \right|\ - 2 \left[\frac{1}{x^{2}}- \frac{\tan^{-1} (x^{2}-1)}{x^{2}} \right]
Is it correct ?
1http://targetiit.com/latex/editor.php?target=message&html
1nihal ,the best way z the graphical approach,the graphical meaning of integration.we'll discuss it in class. Waise maine tmhe hint de diya hai
10∫2pie !cosx- sinx!
! ! REPRESENT MODULUS....
I HAVE GOT SOME IDEA BUT IT IS TOO LONG....
1abe nihal, dude this thread z realy good n helpful,dont close or try to avoid this thread, i m with u man.
23# 8
1] ∫dx1+tanx = ∫cosxsinx+cosxdx = ∫cosx+sinx + cosx - sinx 2(sinx+cosx)
= x2 + ∫ cosx - sinx dx2(sinx+cosx)
put sinx+cosx = t
2] ∫1+sinx-1 dx√1+sinx =∫√1+sinxdx - ∫1√1+sinx dx
now use 1+sinx = (sinx2+cosx2)2= 2sin2(x2+Ï€4)
3] put cosx = t
4]∫dxsinxcos3x = ∫sec4xtanx dx = ∫ (1+tan2x)sec2xtanxdx
put tanx = t
5]∫sec3/4x cosec5/4x dx = ∫dxsin5/4x cos3/4x =∫ dxsin5/4xcos5/4xcos3/4xcos5/4 = ∫ sec2xdxtan5/4x
put tanx = t
23#7
1] x3-1 = t3
x2dx = t2dt
so I = ∫ (x3-1)1/3 x5 .dx = ∫t (t3+1)t2dt = ∫t6+t3 dt
2] ex - 1 = t
exdx = dt
dx = dtt+1
I = ∫dtt(t+1)
3] ex+1 = t
exdx = dt
dx = dtt-1
I = ∫t-2t(t+1) dt
4] put sin(x3) = t
11) ∫11+ tanx dx
2) ∫ sinx√1 + sinxdx
3) ∫ cos9xsinxdx
4) ∫ dxsinx.cos3x
5) ∫ sec3/4x . cosec5/4x.dx
1a) ∫ (x3-1)1/3 x5 .dx
b) ∫1ex-1dx
c) ∫1 - ex1 + ex dx
d) ∫x2.sin3(x3).cosx3. dx
11Put tan √x=z thus dz=sec^2 (√x)[1/2√x]dx
Thus I=2∫z^4 dz
=2/5 z^5
=2/5 (tan^5(√x) ).(ans)
1u r right....but i is an imaginary no. and expressing in terms of i
that is, I=12i logx - ix+ i + c
is contradictory......
1WE KNOW,
I=∫dx1+x2= tan-1x + c
now,
I=∫dx1+x2= ∫dxx2-i2
or, I=12ilog(x-ix+i) + c
1put x=z2 so dx=2zdz
or I=2∫tan4zsec2zdz
now put, tanz=t so dt=sec2zdz
or I=2∫t4dt=25 (tan√x)^5 + c