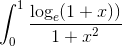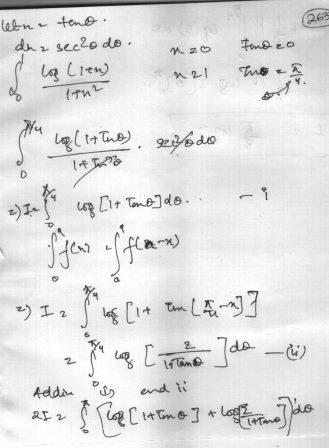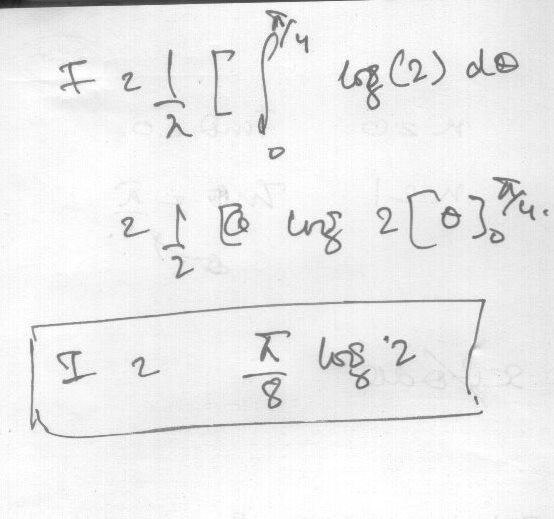Integration

You can also use property of definite integration

$\hspace{-16}Consider: $\bf{I(a) = \int_0^1 \frac{\ln (1+ax)}{1+x^2} \, dx}$\\\\\\ Than, the derivative $\bf{I\hspace{-10}\quad'}$ is equal:\\\\\\ $\bf{I\hspace{-10}\quad'(a) = \int_0^1 \frac{x}{(1+ax)(1+x^2)} \, dx = \frac{2 a \arctan x - 2\ln (1+a x) + \ln (1+x^2)}{2(1+a^2)} \Big|_0^1}$\\\\\\ So $\bf{I\hspace{-10}\quad'(a) = \frac{\pi a + 2 \ln 2}{4(1+a^2)} - \frac{\ln (1+a)}{1+a^2}}$\\\\\\ Hence: $\bf{I(1) = \int_0^1 \left( \frac{\pi a + 2 \ln 2}{4(1+a^2)} - \frac{\ln (1+a)}{1+a^2} \right) \, da}$\\\\\\ $\bf{2 I(1) = \int_0^1 \frac{\pi a + 2 \ln 2}{4(1+a^2)} \, da = \frac{\pi}{4} \ln 2}$\\\\\\ So $\bf{I(1) = \int_0^1 \frac{\ln (1+x)}{1+x^2} \, dx = \frac{\pi}{8}\ln(2)}$