1Yeah, so y=x+sinx will range from -∞ to ∞
Here if U take x=-∞ U get y=-∞
And x=∞ gives y=∞
I didnt get wat U said completely.
If meant sumthing else then plz ask again...
FIND THE INVERSE OF x+Sinx
AND ALSO DRAW THE THE GRAPH OF BOTH THE FUNCTIONS
-
UP 0 DOWN 0 2 47
47 Answers
62f(x)= x+sin x
(a) x-sinx
(b)x+cosx
(c)x-cosx
(d)x+sinx
Answer should be none of these!!!
Where is this question from???? !!!!
f(g(x)) = x
but none of those given in the question will satisfy
moreover the inverse of this I dont think can be written in a "closed form"
1
1dude u r saying through ur graph that the value of whole f(x) will be
please draw the final graph of the f(x)
and
@chetan give the link where it is solved
1DID THE TIITIANS BACKED OF FROM ANY MORE DISCUSSION
OR U WANT TO GO WITHOUT ANYTHING[7]
1itz not a bijective function....dat is proved frm the graph given above.....so how can itz inverse exist........for a function to be invertible it shud b one-one onto.
11miss archana read #9
u r rite
but the graph could me made as of sin-1x and cos-1x
11@kalyan i agree with ur graph the addition will make it something like that only
but the question comes
WHAT IS THE INVERSE OF THAT FUNCTION
FOR ANY DETAILS
I REMEMBER IT IS 1 OF THE TESTS AND THAT TOO FROM #6
1Yeah...in the test the answer is given to be x+sin x with explanation dat it is symmetric about line y=x...n so inverse of f(x) is f(x) itself..!
1no the inverse does not exist in closed form.
mean that the inverse cannot be written as a function ...
1BUT WATS THE LOGIC OF GIVING ONLY 1 QUESTION
IN A TEST
WHOSE ANSWER I AM ASKING FROM YESTERDAY
STILL IF SOME ONE KNOWS IT
PLEASE HELP
66f(x)=x+\sin x
\therefore\ f^\prime(x)=1+\cos x\geq 0
Further the points where the derivative vanishes turn out to be inflection points. Accordingly, f(x) is strictly increasing. So the inverse exists. However, to find an analytical expression, we would need to solve the equation y=x+\sin x for x, which cannot be done in closed form. However, we can implicitly, give the inverse function y=f^{-1}(x) as x=y+\sin y. In the following figure, the solid black curve is the graph of y=x+\sin x while the dotted red curve is the graph of the inverse function given implicitly by x=y+\sin y.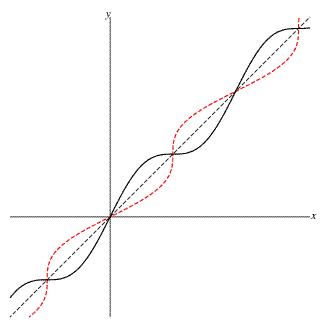
62@archana.. it is a bijective graph
look at its derivative
it is >= 0 at all x
1but Mr Kaymant
the definition os inverse is that it should satisfy
f(f-1x)=x
or we find x in terms of y
but here we can't do anything
so how can u assert that the inverse of x +sinx is x+sinx[7][7][7]
62loney...
if f(x)=y is the function, then the inverse is given by
f(y)=x
66@Lonely and ManiPal,
Did I say that the inverse is x+sinx. What I said is that if y=f^{-1}(x) be the required inverse function, then y is given implicitly by the equation x=y+\sin y. What it means is that for each x, the value of f-1(x) is obtained by solving this equation for y. Like, it we want to find f-1(1), we solve the equation
1=y+sin y
As it turns out, this equation cannot be solved by algebraic means. We need to use numerical methods. Doing so we get y=0.510973 (approx). That means that f-1(1) ≈ 0.510973.
Indeed, we see that
f(f-1(1))=0.999999 (approx),
so that the relation f(f-1(x))=x is indeed true.
Note once again, the inverse exists and it is given implicitly by the equation x = y + sin y. In this equation y is the required inverse function.
1thanx sir 4 ur kind help
i am truely grateful 4 ur help
but please tell me could we get anything like this in JEE
because it deals with approximation
1take the test 5 by abhijeetkumar
http://targetiit.com/tests.html
in the maths section
21thats fine but yaar inv. has to satisy 4 all defined values ne.........