then ..........................
FIND THE INVERSE OF x+Sinx
AND ALSO DRAW THE THE GRAPH OF BOTH THE FUNCTIONS
-
UP 0 DOWN 0 2 47

47 Answers
dude sinx and cosx are also periodic functions
so how can we find their inverses
for a function to have inverse it must be one one and onto
so we take principal value of these functions (by convention )
so what is the point in arguing that its inverse id defined on all the values of R
please draw the graph and find the inverse of the first function!!!!!!!!!!
let y=x+sinx
wel take x as 0....
so y=0
since this passes through d origin and its inverse is a mirror image on y=x...... so even tht also pass through 0,0
so we can eliminate option b and c...
now take ∩/2
y=∩/2+1
point is (∩/2,∩/2+1)
find its mirror image on y=x
and try 2 substitue dat point in a and d....one of them will satisfy......
[1][1][1]
dude good analysis with options
but what if the question was without options ?????????
but i think it could be done in a better way
what about the graph?????
so answer is approximately a.....
Approximately because...
i got d point as (∩/2+1,∩/2)
and when i subsituted in 1
y=∩/2+1-cos1
cos1 is approx 1
so y=∩/2
so ans is approx. A
Dunno about the direct method for inverse, but the graph can be found like this....
The graph for y=x is....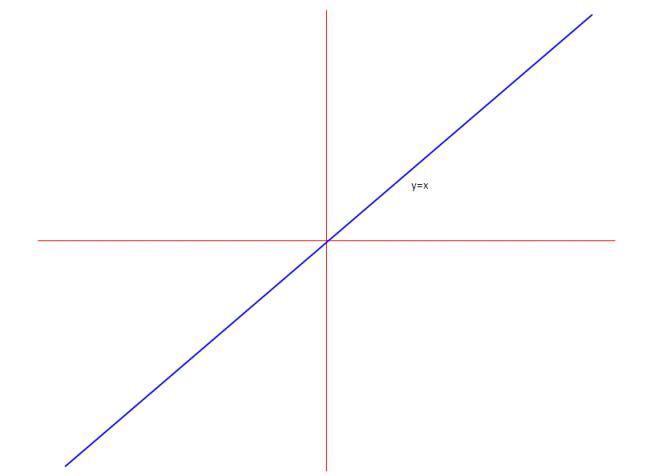
and for y=sinx is....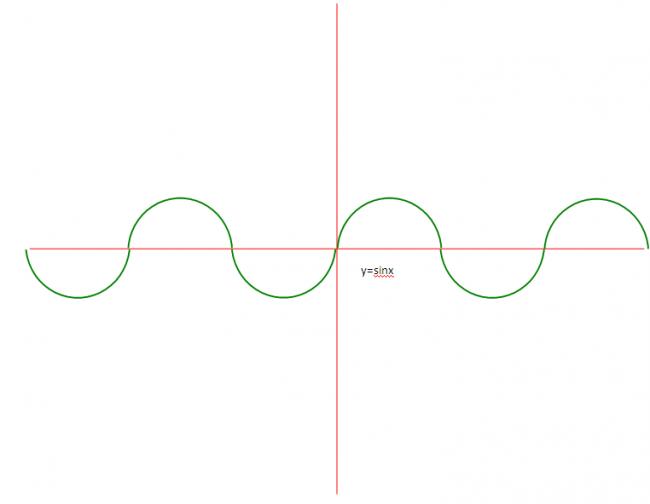
So, the graph for y=x+sin x is......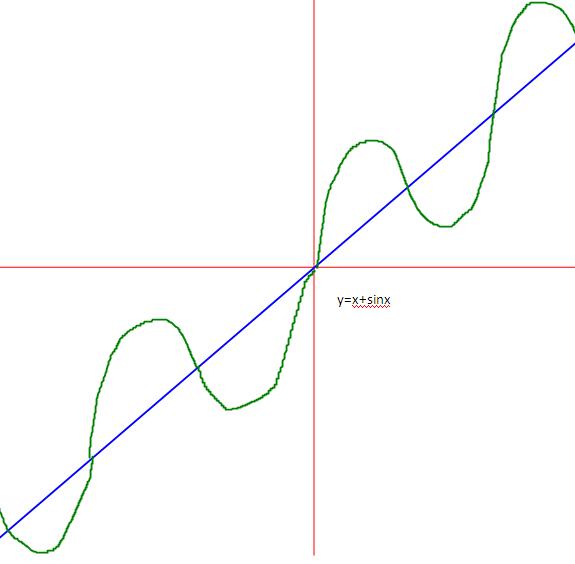
Inverse of this function is its mirror image in y=x which gives...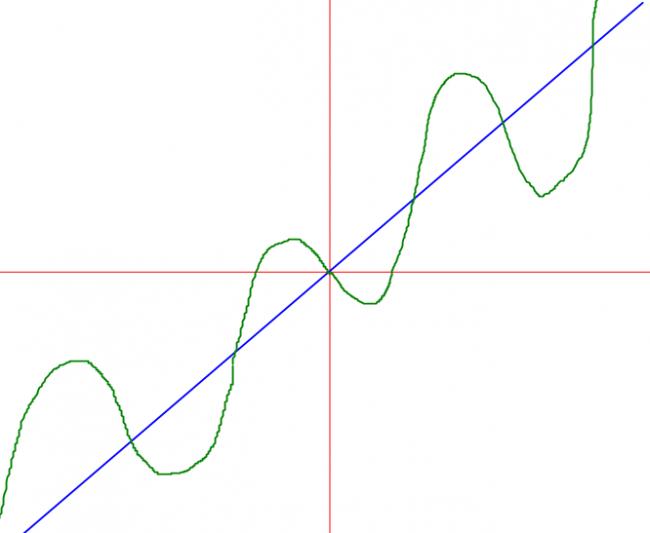
This I suppose is the graph for y= x+cosx
So, the inverse is y=x+cosx
bcos after reflection by y=x sinx will be reflected as -sinx and kalyans graph is correct
Well msp maybe UR right,
coz at 0 here the value is 0, but my inverse gives it 1
So it is y=x-sinx , like U said
I had a doubt about this one,
Now cleared
So,
The graph is as above
and the inverse is y=x-sinx
[339]
@ kalyan
u said


THINK ABOUT THIS AGAIN
THE AMPLITUDE OF SINX WILL ALWAYS REMAIN FROM-1 TO 1 AND X WILL BEGIN 4M -∞ TO ∞
DO READ #6