39
39Consider the function
H(x) = f(x) − f(a) − f(b) − f(a)/(b − a) .(x − a).
As an arithmetic combination of continuous functions the function H is itself continuous.
In fact, the function H can be shown to be differentiable on (a, b) with derivative
H`(x) = f`(x) − f(b) − f(a)/(b − a) ;
Since
H(a) = H(b) = 0 we may apply Rolle’s Theorem to the function H and the interval [a, b].
We conclude there
is some c in (a, b) for which H`(c) = 0,
i.e. f`(c) − f(b) − f(a)/(b − a) = 0.
This completes the proof of the theorem. !
 62
62I think the tougher one is to prove rolle's theorem..
what say?
 11
11Rolle's theorem is just a special case of LMVT no bhaiya ??
so we can say that b555 almost proved rolle's as well.
 19
19rolle's theorem is valid for a function such that
1) f(x) is continuous in the closed interval [a,b]
2) f(x) is differentiable in the open interval (a,b)
3) f(a)=f(b)
so generally two cases arise in such circumstances :
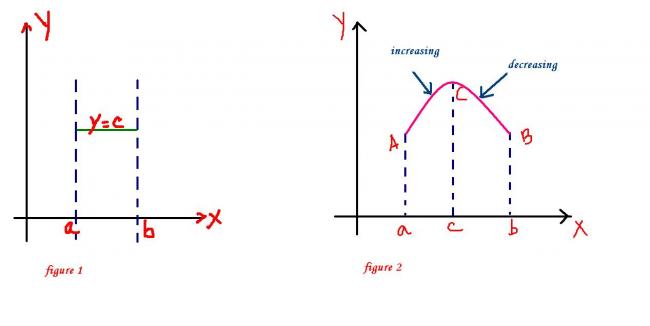
case 1:f(x) is constant in the interval [a,b],,,,,,then f'(x)=0 for all x in the closed interval..........hence rolle's theorem follows and we can prove that f'(c) =0 where a<c<b
this is depicted in figure 1
case 2: f(x) is not constant in the interval [a,b]....and since f(a)=f(b) the function should either increase or decrease when (x) takes values slightly greater than (a) .
now, let f(x) increase for x>a......since f(a) =f(b), then the function must cease to increase at some value x=c and decrease upto x=b
clearly x=c has the max value.
now, let (h) be a small positive quantity from the definition of maximum value of a function ,
f(c+h) -f(c)>0 and f(c-h) - f(c) <0
thus , {f(c+h) -f(c)}/h < 0 and {f(c-h) -f(c)}/-h >0
so, lim(h->0) {f(c+h) -f(c)}/h ≤0 and lim (h->0) {f(c-h) -f(c)}/-h ≥0..........(#)
but if the two limits are not equal then rolle's theorem cannot be applicable because in such case , RHD at x=c ≠LHD at x=c
hence f(x) is not differentiable at x=c which contradicts the condition of rolle's theorem
thus the only possible solution arises when the two limits in (#) are equal and each is equal to zero.
which implies that f'(c)= 0 where a<c<b
this case is depicted in figure 2
Hence rolle's theorem is proved
 66
66Proof of Rolle's Theorem:
Since the function is continuous on the interval [a,b], it has a maximum M and minimum m on that interval.
If M=m, the function is constant over the interval so at any point on the interval, we have f'(x)=0 and so the theorem is proved.
Suppose M≠m. Then at least one of m and M must be non-zero. Let M>0. Let this value be attained for x=c, i.e. f(c)=M. Note that c≠a or b, since it is given that f(a)=f(b)=0. Then f(c+δx)-f(c)≤0 for both δx > 0 and δx < 0. Accordingly,
f(c+δx)-f(c)δx ≤ 0 for δx > 0, and f(c+δx)-f(c)δx ≥ 0 for δx < 0.
Since the limit exist at all interior points of the interval, the limit of the above two ratios exist and both are equal to f'(c).
Hence, we get f'(c) ≥ 0 and f'(c) ≤ 0. i.e. f'(c)=0. q.e.d