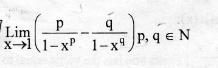limits

Use x^p=[1+(1-x)]^p

take 1-x=y then it becomes lim y->0

Now in the expansion of (1+y)^p use the first 3 terms..

You will get the answer...

\\\frac{p}{1-x^p}-\frac{q}{1-x^q}=\frac{p}{1-(1+t)^p}-\frac{q}{1-(1+t)^q} \\=\frac{p}{1-(1+pt+p(p-1)/2t^2)}-\frac{q}{1-(1+qt+q(q-1)/2t^2)} \\=\frac{1}{t+(q-1)/2t^2}-\frac{1}{t+(p-1)/2t^2} \\=\frac{1}{t}\frac{(p-q)/2\times t}{(1+(q-1)/2t)\times (1+(p-1)/2t)} \\=\frac{(p-q)/2}{(1+(q-1)/2t)\times (1+(p-1)/2t)}

as t tends to zero, the above expression tends to (p-q)/2

yaar am leaving for Durgapur..

You focus on Physics..

See some of the QOD's and anant sir's posts in physics.

I am sure that is going to help you [1]

Will post them tomorrow.