3i can give u an example where the sandwich theorem is applied
x-1≤[x]≤x
[] shows GINT
106i never said anything abt continuity sky.
BTW, can anyone explain me sandwich theorem?
1lim (e^1/x - 1)/(e^1/x + 1)
x-->0
∞/∞ form.
use L'hospital.
limit=1.
------------------------------------------------------------------------------------------------
by traditional method,
LHL:
x-0 = -h.
lim h->0 [(e^1/h - 1)/(1/h)]/[(e^1/h - 1 + 2)/(1/h)]
=1. [lim x->0 (e^x-1)/x =1 ]
similarly RHL will also be 1.
so limit=1.
1@asish,,, u din tell!! i told akand... he was telling something about comtinuity...
62lim (e^1/x - 1)/(e^1/x + 1)
x-->0+
e1/x>>1
hence the limit will be 1
when
lim (e^1/x - 1)/(e^1/x + 1)
x-->0-
e1/x will be close to 0
hence limit will be -1
SO RHL=1
LHL=-1
Hence the limit does not exists
1coz u made a mistake sumwher..........a silly one i suppose...........k wats the answer 4 d given ques??? limit doesnt exist eh?
1sky, if u take RHL then
x-->0_ ==> e^1/x = e^-∞ = 0
then limit = -1/1 = -1
-----------------------------------------------------------------------------------------------------
LHL is not x->0-
is it?
it is jus checking the limit at the nearby region of x=0... but on the left hand side.
31) Lt {x}/tan{x}
x→0
Solution....
RHL=Lt x-[x]/tan(x-[x]) =Lt x/tanx....as when x→o+,[x]→0 !!
x→0+ x→0+
thus RHL=1
LHL=Lt x-[x]/tan(x-[x])=Lt x+1/tan(x+1)....since when x→0-,[x]→--1
x→0- x→0-
thus LHL=Cot1
thus LHL≠RHL...THUS LIMIT DOEST NT EXIST !!
1for first question limit does not exixt........
because in rhl you find 1............
but in lhl you will find
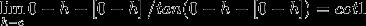
you can use box0-h when h-o is -h-1.......... you can obtain this result........
1{0-h} is not h............so LHL not eqaul to RHL..............im not sure
106yes i meant that if u evaluate using LHL and RHL then RHL = 1
but LHL is not 1 hence i think limit wont exist
106see another one:
lim (e^1/x - 1)/(e^1/x + 1)
x-->0
If you divide e^1/x throughout and then evaluate limit, u will get the answer as 1 but if u take LHL and RHL then LHL=1 and RHL=-1.
We are taught to just put the value first to evaluate the limit, the limit then if its indeterminate then to simplify it..but here, if we do so, answer is wrong!!!! so how do we do it?
