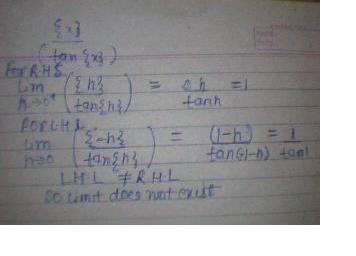1Q3. 1/8?
lim x→0 [(sin signum(x))/signum(x)] where [] is GIF?? options are given
(a)0 (b)1 (c)1/2 (d) does nt exsist
Q2 Let {x} denote the fractional part of x then lim x→0 ({x})/tan({x}) is equal to=??
Q3. lim x→0 (1-cos(1-cosx))/x4=?
-
UP 0 DOWN 0 0 12
12 Answers
1ajoy cn u plz explain hw u gt it....but i hope u hve nt used L hospital rule
106no need to use LH rule directly..
u can write (1-cosx) = 2sin2(x/2) and evaluate
1is d ans for d first one 0?????????
and yes jangra2819.........please explain ur ans.......
1i thnk ans of 1st one is 0 bcz signum(x)=1,-1,0 so [sin(1)/1]=0 nd [sin(-1)/-1]=0 nd sme fr sin o nd 1<∩/2 so [sin (1)/1] is 0
11) ans (a)
LHL=RHL= [(sin1)/1]=0
2) ans --> doesn't exist... since LHL= 1/tan1 and RHL=1
3) lim 1 - cos(1-cosx)(1-cosx)2 . {(1-cosx)/x}2
x-->0
=(1/2). 1/4 = 1/8
remember lim 1-coskxx2= k2/2
x-->0