i read in a book that,the expansion series of tan x is derived by term by term division of expansion series of sinx by cosx
btw do u knw how to derive expansion series of sinx or cosx ?
How do we find the next term in these series? I mean what is the logic behind every successive term?

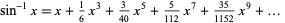
It is not an AP or GP.
Please help
i read in a book that,the expansion series of tan x is derived by term by term division of expansion series of sinx by cosx
btw do u knw how to derive expansion series of sinx or cosx ?
The logic behind this is, we can find a function by finding its derivative at each point and plotting them. This is known as Taylor's theorem.
You might want to read the following articles for further readings about them:
http://en.wikipedia.org/wiki/Taylor_series
http://en.wikipedia.org/wiki/Taylor%27s_theorem
You could use a Taylor expansion for those functions. You'll do Taylor and Maclaurin series in engineering mathematics for sure. Sometimes you'll see those topics included in AIEEE coaching manuals as well, so no harm in knowing them!
For example, I'll derive the series of sin(x) for you. For the function sin(x + h) such that h > 0 is very small(meaning in neighbourhood of x), we put h = 0 and differentiate the function that many number of times the number of terms you want in the series.
f(x) = sin(x)
f'(x) = cos(x)
f"(x) = -sin(x)
f"'(x) = -cos(x)
fIV(x) = sin(x)
And so on.
f(x + h) = f(x) + hf'(x) + h²2!f"(x) + h33!f"'(x) + .....
So sin(x + h) = sin(x) + hcos(x) - h²2!sin(x) - h33!cos(x) + .....
This was the normal way to represent a Taylor series.
Now write x = h + (x - h).
Let X = h, H = x - h.
f(h + (x - h)) = f(h) + (x - h)f'(h) + (x - h)²2!f"(x) + ...
So sin(h + (x - h)) = sin(h) + (x - h)cos(h) - (x - h)²2!sin(h) + ....
Now we can find the series at X = 0 or h = 0.
sin(h + (x - h)) = 0 + x - x²2! * 0 - x33! * 1 + .....
= sin(x).
So sin(x) = x - x33! + ...
and so on. The series expansions that we use are series expansions in the neighbourhood of the point X = zero.
Hope this helped! You could similarly find out the expansion of sin-1(x).
Post in my chatbox if you can't find it yourself or have problems..
Thanks alot Pritish bro.
My question was something else. I meant that how do we remember the coefficients of successive terms?
In the example of tanx,
is there any particular rule by which the coefficients can be written (without deriving)? ( 1/3 , 2/15 etc)
Do we have to byheart them as it is?
I think, back in FIITJEE, we derived the series for tan(x) by dividing series of sin(x) and cos(x)...though I don't remember how that came about. If I find the text I'll post it here.