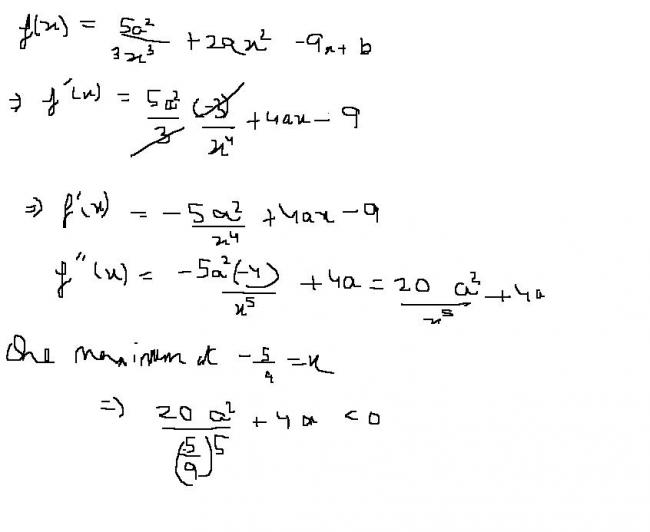1Edited
For what real values of 'a' and 'b' all the maximum of the function
f(x)= (5a2/3x3) + 2ax2 - 9x +b
are positive and maximum is at point x0=-5/9??
-
UP 0 DOWN 0 0 6
6 Answers
1I have half-solved the question, but need someone to give me its proper solution.
1f'(x)=0
=> x= 9/5a, 1/a
Case 1
when a<0;
then maxima occurs when x=1/a
=> 1/a =-5/9
=> a= -9/5
Minima therefore exist when x=9/5a=1
=> f(1)>0 when a =-9/5
=> 5a2/3+2a-9+b>0
Putting value of a
=> b> 36/5
Case 2
f(25/81)>0
=> (5*81*81*25*25)/(3*81*81*81*25*25) + (2*25)/81 - (9*25)/81 + b >0
→ b>400/243
So, if a=-9/5, b>36/5
If a=81/25, b= 400/243