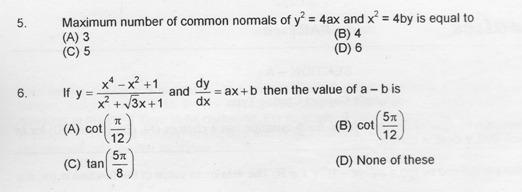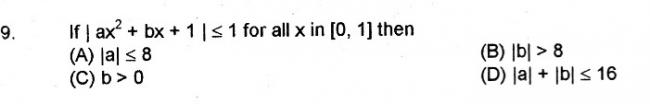1708Vivek i also have Lengthy Method.........
\hspace{-16}$Here $\mathbf{\frac{z_{1}^2}{z_{2}z_{3}}+\frac{z_{2}^2}{z_{3}z_{1}}+\frac{z_{3}^2}{z_{1}z_{2}}+1=0}$\\\\\\ $\mathbf{z_{1}^3+z_{2}^3+z_{3}^3=-z_{1}.z_{2}.z_{3}}$\\\\\\ $\mathbf{z_{1}^3+z_{2}^3+z_{3}^3-3z_{1}.z_{2}.z_{3}=-4z_{1}.z_{2}.z_{3}}$\\\\\\ $\mathbf{\left(z_{1}+z_{2}+z_{3}\right).\left\{\left(z_{1}+z_{2}+z_{3}\right)^2-3\left(z_{1}z_{2}+z_{2}z_{3}+z_{3}z_{1}\right)\right\}=-4z_{1}z_{2}z_{3}}$\\\\\\ Now Let $\mathbf{z_{1}+z_{2}+z_{3}=x}$ and $\mathbf{\mid z_{1}\mid = \mid z_{2}\mid=\mid z_{3}\mid = 1}$\\\\\\ Then Equation is $\mathbf{\frac{x^3}{z_{1}z_{2}z_{3}}-3x\left(\frac{1}{z_{1}}+\frac{1}{z_{2}}+\frac{1}{z_{3}}\right)=-4}$\\\\\\ Now $\mathbf{\bar{z_{1}}+\bar{z_{2}}+\bar{z_{3}}=\bar{x}\Leftrightarrow \bar{x}=\frac{1}{z_{1}}+\frac{1}{z_{2}}+\frac{1}{z_{3}}}$\\\\\\ So $\mathbf{\frac{x^3}{z_{1}z_{2}z_{3}}-3x\bar{x}=-4\Leftrightarrow \mid x\mid^3 = \left|\;\; 3\mid x \mid^2-4\;\;\right|}$
\hspace{-16}$\bullet\;\; $\mathbf{3\mid x \mid^2-4\geq 0}$, Then \\\\\\ $\mathbf{\mid x \mid^3=3\mid x \mid^2-4\Leftrightarrow \mid x \mid =2>\frac{2}{\sqrt{3}}}$\\\\\\ \bullet\;\; $\mathbf{3\mid x \mid^2-4< 0}$, Then \\\\\\ $\mathbf{\mid x \mid^3=3\mid x \mid^2-4\Leftrightarrow \mid x \mid =1<\frac{2}{\sqrt{3}}}$\\\\\\ So all possible values of $\mathbf{x = \mid z_{1}+z_{2}+z_{3}\mid =2+1=3}$
119) This is pretty easy btw
Simply writing: a=2f(1)-4f(12)+2f(0)
b=4f(12)-f(1)-3f(0) simplifies things
1q9) is a nice one
write as -1<ax^2+bx+1<1
using rhs ineq u get x(ax+b)<0 now since x s bet 0 and 1 x is always +ve therefore
ax+b<0 ax<-b and now use lhs ineq to get
0<ax^2+bx+2
now let its roots be r1 and r2 now u have cases here first if r1 and r2 are both imag or disc <0 then it is obviusly true since at o the value is 1
if both are real then let r1 be the smaller and r2 the bigger
either r1>0 then it is true or 0>r2 in eithe of the two cases u have equality now solve it\
actually this is another olympaid question copied form challenges and thrills in pre college math and modified a bit
1
varun.tinkle
·2012-02-17 03:09:47
q 6) is definietly out of portion since it uses a very trivial number theory formula which states that x^2+y^2 can only have a factor of the form 4k+3 if both x and y are idvisible by the same prime factore or to cut the story short both x and y have to be multiple of 7 (though it can be done withouth that too observing the modulus i beleive it is too much to ask in jee type test)
for multiple of 5 by observing basic congruences u can only have numbers of form
5k,5k,
5k+1,(5k+2,5k+3)
5k+4(5K+2,5K+3)
now the prob can be easily calc
1
varun.tinkle
·2012-02-17 03:04:17
q2) maybe a silly mistake but here it goes
write z as x+iy
thereofre x+i(y+1)/x+i(y-1) rationaise the denominator and write it as (x+i)^2-iy^2/something doesnt matter so the real part becomes x^2+y^2-1 +2ixy now equate that either real part =imag or -real part =imag my eq is coming as (x-1)^2+y^2=2 and (x+1)^+y^2=2
11
Devil
·2012-02-13 06:46:58
1)
http://www.targetiit.com/iit-jee-forum/posts/integer-function-equation-11657.html
262Q1) area of the region bounded by the locus of z satisfying argz+5iz-5i = ±pi/4
i am getting 75pi , ans given is 75pi +50
262
Aditya Bhutra
·2012-02-06 02:21:37
nice soln man111 !!
but i am still looking forward to a more crisp soln. to the complex no. question .
if you could please post the soln. to Q9.
1the 2nd question is cot(5Ï€/6)
1708
man111 singh
·2012-02-05 07:03:34
for (9) (a) and (d)
for (probability) = 9/(1225)
1057for the last question....
let S=1+122+132+142..... upto ∞
let x=1+132+152+172..... upto ∞
let y=122+142+162..... upto ∞
now it is clear that taking 14 common in y we get y=S4
and alrdy S=x+y
therefore x=S-y=3S4
now the question is to find out Sx-y
which is equal to S0.75S-0.25S which is equal to 2... :)
1708
man111 singh
·2012-02-05 06:31:28
$Here $\mathbf{y=\frac{x^4-x^2+1}{x^2+\sqrt{3}x+1}}$\\\\\\ $\mathbf{x^4+1-x^2=(x^2+1)^2-(\sqrt{3}x)^2=\left(x^2+\sqrt{3}x+1\right).\left(x^2-\sqrt{3}x+1\right)}$\\\\\\ So $\mathbf{y=\left(x^2-\sqrt{3}x+1\right)}$\\\\\\ So $\mathbf{\frac{dy}{dx} =2x-\sqrt{3}=ax+b}$\\\\\\ So $\mathbf{a=2\;\;,b=-\sqrt{3}}$\\\\\\ So $\mathbf{a-b = 2+\sqrt{3}}$\\\\\\ Now $\mathbf{\cot \left(\frac{\pi}{12}\right)=\frac{\sqrt{3}+1}{\sqrt{3}-1}=2+\sqrt{3}}$\\\\\\ So $\mathbf{a-b = \cot \left(\frac{\pi}{12}\right)}$
71The one has answer 5 i.e., Maximum no. of common normals is 5.
Merge the equation of normal for two parabolas , and you'll get a 5th get equation of m.
71
Vivek @ Born this Way
·2012-01-31 21:17:31
Using the fact that every set of natural nos. has a smallest element, We'll start with f(1)=1. However this will fail to satisfy the conditions given. The next and required possibility is f(1)=2, and which obviously satisfied all given conditions. This will give f(2)=3.
7
Sigma
·2012-01-31 06:47:35
For q 9 anything to do with Rolle's Theorem?
262
Aditya Bhutra
·2012-01-31 06:39:30
thnx ketan and vivek .
@vivek- it is 3 . solution ?
71
Vivek @ Born this Way
·2012-01-30 21:32:59
I have a bit long method for this. So, I'll wait for any elegant solution for this.
Pass any circle through the points i and - i ie.., the line joining these points is a chord of a circle which is the locus of z. Certainly this chord will subtend an angle Î /2 at center and hence Î /4 at the cicumference as according to condition.
Now you can easily find the radius of circle, length of arc.
Take the numerator as A and denominator as B, then see that A-B=A/2.
