wats the function ?
Q1)
The function f : R → R defined by
f(x)=x3+x2
is
(a) one to one
(b) onto
(c) one to one and onto
(d) neither one to one nor onto
Q2)
The function
f(x)= x2/|x| if x is not = 0
= 0 if x=0
(a) is not continuous at x = 0
(b) continuous at x = 0, but not differentiable
(c) differentiable once, but not twice
(d) differentiable infinitely many times
Q3)
The differential equation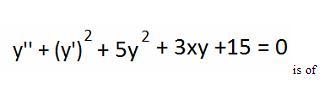
(a) degree 1 and order 2
(b) degree 2 and order 1
(c) degree 1 and order 1
(d) degree 2 and order 2
Q4)
Let A, B and C be 3 matrices of order n X n such that ABC = I, where I is the identity matrix of order n, then
(a) A, B and C are always invertible
(b) A, B and C are not necessarily invertible
(c) B is invertible
(d) A is always invertible
-
UP 0 DOWN 0 0 14

14 Answers
shouldnt 3 be a abhirup?
2nd order of derivative is max and the highest power of that is 1.
∫1-1x21+1xdx (limits from 1/2 to 2)
=∫dzz (limits from 5/2 to 5/2) = 0......where z=1+1x
whats the flaw in dis 1....first confirm yourself that there is a flaw as the integration of the original function cannot be 0
ans 1)
function has two roots 0 and -1 . thus it is not one-to one . but ti's range is R .
thus is onto .
Option B
3)as far as 3 question is concerned the option wud be (a)
2)ans of second one wud be(b) as
{-x,x<0
f(x)={0,x=0
{x,x>0
so ans (b)
1)ans of (1) cannot be (c) as if f(xi)=f(x2)
means x1sq+x2sq-x1-x2+x1x2=0
not x1=x2