1hey i dunno wats jenson ineqaulity
can u giv soln wrt maxima and minima coincept(related to calculus)bec this is a q from my calculus modules
For any acute angled \Delta ABC
find the minimum value of \frac{sinA}{A}+\frac{sinB}{B}+\frac{sinC}{C}
-
UP 0 DOWN 0 0 4
4 Answers
62sin A-A2+cos AA
cos A-A2+2sin A-A3-cos AA2-sin AA
I dont see how i prove convexity or concavity.. but somehow my gut says that this has to do with jenson's inequality.!
1jensen's inequality
the concavity is shown by a familiar graph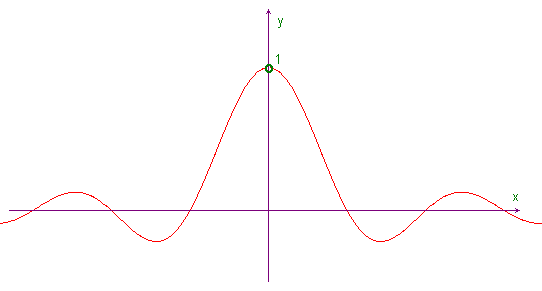 
the roots are same as roots of sinx ...
so we can say 0≤x≤π/2 function is concave
\frac{\sin A}{A}+\frac{\sin B}{B}+\frac{\sin C}{C}\leq 3\frac{sin\left(\frac{A+B+C}{3} \right)}{\frac{A+B+C}{3}}=\frac{9\sqrt{3}}{2\pi}
11actually jensen inequality is more of calculus ,
if the curve is convex then the mean of f(x)>f(mean x),inequlity is flipped for concave
similarly we can generalise mean to weighted mean also [1]