solve the following :
(1) find the period of |sin3 x/2| + |cos5 x/2|
(2)if f:R->R and g:R->R be two one one and onto functions such that they are the mirror images of each other about the line y=a and h(x) = f(x) + g(x) , then h(x) is :
(a) one one and onto (b) only one one but not onto
(c)only onto but not one one (d)neither one one nor onto
106Q2.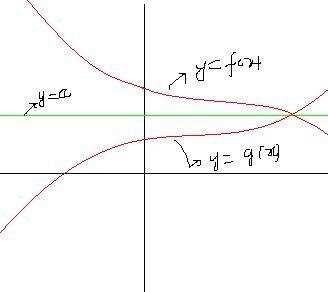 
Consider f1(x)=f(x)-a and g1(x)=g(x)-a
Then if u draw a simple graph (by shifting the two curves downward by 'a') then you will see that f1(x)= -g1(x)
as both graphs will be symmetrical about x-axis.
So, f(x)-a = -[g(x)-a]
==> f(x)+g(x) = h(x) = 2a
So h(x) is neither one-one nor onto
