\text{if we substituite } 1+a^2-2a\cos x =t \\ \text{ then the integral boils to }\\ \int_{a_1}^{a_2}{\frac{\log (t)dt}{\sqrt{t-a_1}\sqrt{t-a_2}}}\\ \text{now we can go by parts}\\ \text{here }a_1=(a-1)^2 \ and \ a_2=(a+1)^2
but how to go about by che's hint ?
plz solve
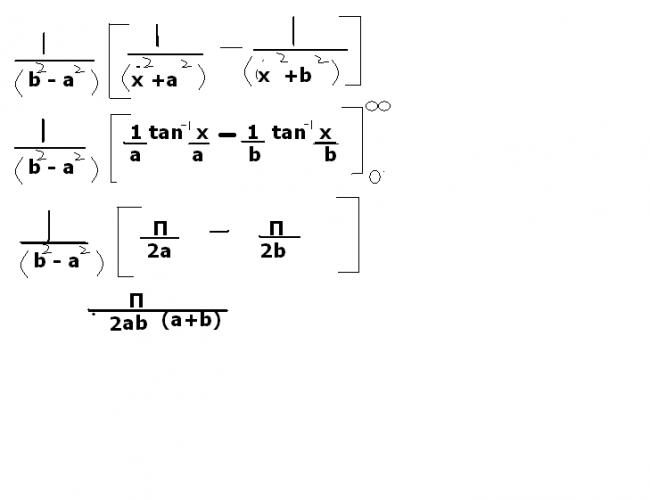
1) \int_{0}^{\infty}{\frac{1}{(x^2+a^2)(x^2+b^2)}}dx
2) \int_{0}^{\pi}{log(1-6cosx+9)}dx
3)\int_{0}^{1}{\frac{x^{a-1}-x^{-a}}{(1+x)logx}}dx
-
UP 0 DOWN 0 3 31

31 Answers
well this was solved beautifully by nishant and theprophet sir
http://targetiit.com/iit-jee-forum/posts/prove-the-following-11283.html
I=\int_{0}^{1}{\frac{x^{a-1}-x^{-a}}{(1+x)lnx}dx} \\=\int_{0}^{1}{\frac{x^{a-1}}{(1+x)lnx}dx}-\int_{0}^{1}{\frac{x^{-a}}{(1+x)lnx}dx} \\ \\Substitute\: x=\frac{1}{t} \: in\: second\: integral \\we\: get: \\=\int_{0}^{1}{\frac{x^{a-1}}{(1+x)lnx}dx}+\int_{1}^{\infty}{\frac{t^{a-1}}{(1+t)lnt}dt} \\=\int_{0}^{\infty}{\frac{x^{a-1}}{(1+x)lnx}dx} \\Consider:\: f(a)=\int_{0}^{\infty}{\frac{x^{a-1}}{(1+x)lnx}dx} \\\frac{\partial f}{\partial a}=\int_{0}^{\infty} {\frac{x^{a-1}}{1+x}dx} \\Now\: substitute\: x=\frac{1}{z}-1 \\You\: will\: get: \\\frac{\partial f}{\partial a}= \int_{0}^{1}{z^{-a}(1-z)^{1-a}}=\beta(1-a,a)=\pi cosec(a\pi) \\f(a)=-ln\left|cosec\pi a+cot\pi a \right|+c \\f\left(\frac{1}{2} \right)=0 \\or,\: c-ln\left|cosec\frac{\pi}{2} +cot\frac{\pi}{2} \right|=0 \\or,\: c=0 \\Therefore: \: I=-ln\left|cosec\pi a+cot\pi a \right|
Beta function is not in JEE syllabus. I have used a property of beta function in my solution only because I was not able to evaluate the integral in any other way.
Do point out any mistake in my solution.
Consider integrating \,\phi(\alpha)=\int_0^\pi\,\ln(1-2\alpha\cos(x)+\alpha^2)\;dx\,
now,
\begin{align} \frac{d}{d\alpha}\,\phi(\alpha)\, &=\int_0^\pi \frac{-2\cos(x)+2\alpha}{1-2\alpha \cos(x)+\alpha^2}\;dx\, \\ &=\frac{1}{\alpha}\int_0^\pi\,\left(1-\frac{(1-\alpha)^2}{1-2\alpha \cos(x)+\alpha^2}\,\right)\,dx\, \\ &=\frac{\pi}{\alpha}-\frac{2}{\alpha}\left\{\,\arctan\left(\frac{1+\alpha}{1-\alpha}\cdot\tan\left(\frac{x}{2}\right)\right)\,\right\}\,\bigg|_0^\pi. \end{align}
As x varies from 0 to \pi, \left(\frac{1+\alpha}{1-\alpha}\cdot\tan\left(\frac{x}{2}\right)\right)\,varies through positive values from 0 to infinity when -1<\alpha <1 and \left(\frac{1+\alpha}{1-\alpha}\cdot\tan\left(\frac{x}{2}\right)\right)\, varies through negative values from 0 , -\infty when \alpha < -1,or,\alpha >1
Hence,
\\arctan\left(\frac{1+\alpha}{1-\alpha}\cdot\tan\left(\frac{x}{2}\right)\right)\,\bigg|_0^\pi=\frac{\pi}{2}\, when -1<\alpha <1
\\arctan\left(\frac{1+\alpha}{1-\alpha}\cdot\tan\left(\frac{x}{2}\right)\right)\,\bigg|_0^\pi=-\frac{\pi}{2}\, when \alpha < -1,or,\alpha >1
Therefore ,
\frac{d}{d\alpha}\,\phi(\alpha)\,=0\, when -1<\alpha <1
\frac{d}{d\alpha}\,\phi(\alpha)\,=\frac{2\pi}{\alpha}\, when \alpha < -1,or,\alpha >1
Upon integrating both sides with respect to wrt \alpha we get \phi (\alpha ) = C_{1} when -1<\alpha <1
and \phi (\alpha ) = 2\pi ln\left|\alpha \right|+C_{2} when \alpha < -1,or,\alpha >1
C1 can be determined by setting \alpha = 0
we get C1 = 0
to determine C2 we substitute http://latex.codecogs.com/gif.latex?\alpha%20=\frac{1}{\beta%20} where -1<\beta <1
\begin{align} \phi(\alpha) &=\int_0^\pi\left(\ln(1-2\beta \cos(x)+\beta^2)-2\ln|\beta|\right)\;dx\, \\ &=0-2\pi\ln|\beta|\, \\ &=2\pi\ln|\alpha|\, \end{align}
hence we can conclude \phi (\alpha ) = 0,-1<\alpha <1 and
\phi (\alpha ) = 2\pi ln\left|\alpha \right| when,-1>\alpha ,\alpha >1
AArey sir, put the limits....\int_{0}^{\pi}{\frac{dx}{a+bcosx}} Here a=k and b=1.
Sir, but that's an integral of the form
\int \frac{dx}{a+bcosx}, which here turns out to be \frac{1}{\sqrt{k^2-1}}cos^{-1}\left[\frac{1+kcosx}{k+cosx}\right] _{0}^{\pi}....sorry if I'm making some silly error - but pls ppoint it out to me.
@soumik
I was wondering how you got that integral in the second step in terms of cos inverse.
Are these things at all are reqd?
I(k)=\int_{0}^{\pi}{ln(k+cos\alpha)d\alpha}
I'(k)=\int_{0}^{\pi}{\frac{d\alpha}{k+cos\alpha}}=\frac{1}{\sqrt{k^2-1}}\left\{cos^{-1}\left(\frac{k+1}{k+1} \right)-cos^{-1}\left(\frac{1-k}{k-1} \right) \right\}
From which we get
I'(k)=\frac{-\pi}{\sqrt{k^2-1}}
I(k)=-\pi ln|k+\sqrt{k^2-1}|+c
For figuring out the const. we have for k=1, I(1)=2\int_{0}^{\frac{\pi}{2}}{ln(sin\alpha) d\alpha}=2\pi ln \left(\frac{1}{2} \right)
Thus the const. c=2\pi ln\left(\frac{1}{2} \right), and we need I\left(\frac{10}{6} \right).
Many might be wondering what the heck I\left(\frac{10}{6} \right) - let me clear that.
See ln(10+6cos\alpha)=ln6\left(\frac{10}{6}+cos\alpha \right)=ln6+ln\left(\frac{10}{6}+cos\alpha \right).....
Finally plugging the values, we have the ans as \boxed{I=2\pi ln3} - as said by kaymant sir.
Done!!! [56]
sir i meant the bracket in second last line is closed after the integration is performed
sorry for that
actually these latex symbols made me so confused about placing
i hope its correct now
actually i didnt mean taking summation outside
i meant taking integral inside
no karna.. the second last step, you cant take the summation outside!
Think something better... slightly...
I think you have made a mistake in positioning of the bracket.
2 . problem given in arihant
substitution is given in
arihant indefinite integrals
solved examples
PAGE.NO --84
EXAMPLE--6
EDITION -2010-11
NEEDS A BIT KNOWLEDGE OF COMPLEX NO.S AND LOG .SERIES
I DID NOT KNOW IT !!!
THIS WAS TOLD TO ME BY QWERTY
For the 3rd sum, differentiate w.r.t a, then evaluate the integral, followed by an indefinite one w.r.t. a.
no not that way.. the better way was to take x = pi-x
then add both the integrals to find 2I..
Then go about using some trick to prove that there is some kind of a reccursion!
in the first question use partial fractions...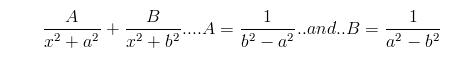
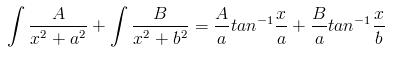 ..
..
on putting the limits u will get..
(A/a + B/b)Ï€/2...
Yes it was one which was replied completely by prophet sir.. let me try to search that one..
Yes.. it could be done without that substitution. I think it has already been done in this forum itself. But I am unable to find that particular thread.
For 2) use the following general result:
\int_0^\pi \ln(1-2a\cos x+a^2)\ \mathrm dx =\left\{\begin{matrix} 0 & \text{ if } |a|\le 1\\[2ex] 2\pi\ln |a| & \text{ if } |a|>1 \end{matrix}}\right.
to get the required result as 2\pi \ln 3
awesome substitution in 10.. (I am not sure if i would have thought of the same :)
tapas.. i agree to the other comments.. I dont knwo what you are trying to prove by posting these fro mathematica....
Please try not to use this on the site.. It makes absolutely no sense at all...
@tapas......
i think it has been reminded to u a lot of times NOT TO USE MATHEMATICA ON THIS SITE [16][16]
In the 2nd one have you written 1 + 9 instead of 10 deliberately or is there a typo ?