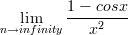1philip d q posted by u is rite
n d answer's 2
:)
cheero~
Q1\lim_{n\rightarrow infinity}(\frac{1}{n^{100}}\sum_{r=1}^{n}{r^{99}})
-
UP 0 DOWN 0 0 67
67 Answers
11@RICHA
MERE KHYAAL SE QUES 4 MEIN KOI PROBLEM HAI
IS MEIN GRAPH OPENING UPWARDS HAI TO
WHAT IS THE LOGIC OF ASKING THE QUESTION
ITS MAXIMUM VALUE IS BOUND TO BE ∞
WHICH MAKES THE SITUATION MORE COMPLICATED [2]
1ARREY WHEN WE dont know which or rather wat is the correct question how can u keep on guessin evrything girls..
leave this for now... until eureka comes
othewise i announce ( [4][4] forgive the expression)
that post 49 is correct question and subhash's soln is good
1answer's 2 ?
(waise dkeha jaye toh us fucntion ki max valueinfi hogai coz thats a upward parabola uski minimum value x=1/12 par hai u dn egt max der )
ya so philip itz rite d q posted by u
11Q2
@tapan
as iit is nearing
so to be true these expansions r to be made and solved which involves a lot of time
(better if u remember them)
(but no one does as they r not used frequently)
so i suggest the juniors to solve them as it basically deals with expansions and binomial
but as far as i am concerned this is a long and lenghthy subjective problem
i don't stop u but i thought it would be fruitful t leave it to the juniors
sorry eureka(no disrespect for these good ques) but i thought this was important to know
1@ EUREKA
i dont know a lot about Reimanns sum...........If it is that thing in Q2 then I will surely delete it...
wat are u talking about eureka........ if yu dont know reimanns sum how did u deduce the post very above my post before this one..
and how did u solve the first prob......
wahi integrand mein badalne wale mthod ko reimanns sum kehte hain
24@ i dont know a lot about Reimanns sum...........If it is that thing in Q2 then I will surely delete it....[1][1]
24well manipal.......dont say sorry for anything.......
@tapan.hint for Q2 ::use fact that \lim_{n\rightarrow infinity}\frac{S_k(n){}}{n^{k+1}}=\frac{1}{k+1}
1am i the only one who is seeing a Reimanns sum in the second question also??
well maybe i am but give me 5 minutes
24Q4Let a is maximum value of function f(x)=\frac{1}{8}(6x^{2}-x^{3}-16)
and r=\lim_{x\rightarrow infinity}\frac{1-cosx}{x^{2}}
Sorry here it is lim x→0
If S=a+ar+ar2+.....∞ find √S
Sorry edited wrongly last nite....now it is OK.......[1][1]
24@ richa......i too havent solved all of them.......some are my doubts while some are just posted here for everyone........
24No tapan that wont be used here in Q2.....a fact will be used ....if u know it then it will be done otherwise...[12]
24Q3 Let An express (1+3-1)(1+3-2)(1+3-4)...............(1+3-2n).
If L= lim An.....then answer these questions
n→∞
Q1 Is L a prime number
Q2 Is 2L a prime number
Q3 Find minimum value of L
Q4 Find maximum value of L
21One thing i know is : S3(n) = [ S1(n) ] 2
thats directly frm the formula..... and v also hav formulae for higher powers.....
If ne1 has more plausible/novel methd, pl. tgell me!!!
21Hope Q2 is not to b solvd by using those formulae for Σ(n3) and Σn and all those ones............
24Q2 LetS_{k}(n)=\sum_{r=1}^{n}{r^{k}} then calculate\lim_{n\rightarrow infinity}\frac{S_1(n)S_5(n)-S_3(n)^{2}{}{}{}{}}{S_7(n){}}
21Q2.
EURE : pl. tell me the rational behind POST # 13
BTW is da ans = 3/7 or sumthin lyk dat?
24mujhe naam nahin pata hai bhai.........reimanns sum ka naam padhkar laga ki yeh cheez syllabus se bahar ki hogi isliye keh raha thaa ki delete kar deta hoon........agar integrand mein badalne ka naam hi reimans hai to theek hai.........[1][1]
24@ tapan.....i dont have proof for it....my brother told me just to remember this result in case of calamity.......
@ philip u r rite
24@ richa i think there is typing mistake there.......it should be x in place of x3
11solution for the problem when x3 was in place of x
answer for Q4 is 1
for the limit in
r=(2sin2x/2)/x2
it comes out to be 1/2
and a=2 which is also pretty easy to find
so answer 1
1arrey fir ye kya eureka
..i dont have proof for it....my brother told me just to remember this result in case of calamity.....
____________________
convert it into integral by multiplying & dividing by n^k+1 in each case it turns out exactly as is written in #13
21my methd 4 Q2 [wrong un though]
divide num and den n^8
Usin formula by eure in post 13
{(S1/n^2)*(S5/n^6) - (S3/n^4)2 }/S7/n^8
ther4 RHS = (1/24 - 1/16)/(1/8) = 1/6 [11] [11]
wat was i doin bloody calc mist.. [222]
THNX EURE formula kam aayi yaar!!!