1jus want to know one thing
how u got this [t].{x} = 1/2 [x]
Number of solns for x between 3 and 15 if \int_{0}^{x}{\left[t \right]}.dt=\int_{0}^{\left[x \right]}{t.dt}
wer [.] is GIF
-
UP 0 DOWN 0 0 5
5 Answers
62This question is same as \\\int_{0}^{[x]}{[t]dt}+\int_{[x]}^{x}{[t]dt}=\int_{0}^{[x]}{tdt} \\\int_{[x]}^{x}{[t]dt}=\int_{0}^{[x]}{\{t\}dt}
so you have
[t].{x} = 1/2 [x]
Now you have to finish it... can you try?
62In the LHS, [t] is constant in the interval [x] to x... so the lHS is simply the integral of 1 over the interval [x] and x multiplied by [t]
so it is [t]{x}
The rhs is to be thought out by you :)
11answer is 0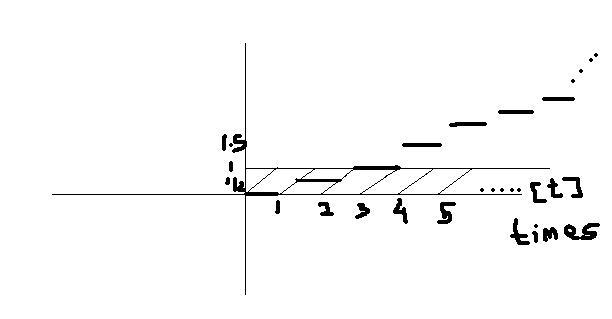
since no intersections after 3 so no solution of x b/w 3 & 15
1@nishant sir ......ok i got it....thanx
@sandipan ans is 12 solns