is it 2 to 14?
a function f:R→R
f(x)=(px2 +6x-8)/(p+6x-8x2)
Find the integral values of p for which the given function is onto .
-
UP 0 DOWN 0 0 9

9 Answers
I will give u a hint..
Think in tems of the neighborhood of the roots of numerator and denominator!
(Good question.. took me sometime to think! :)
you can eqaute it to y and then y should be frm -∞ to ∞.
using quadraic equations property and determinants. ull get 2 to 14.
is there any other method.
Sorry dude for the late reply..
More Hint: (btw this is an interesting question to solve without using differentiation as u said :)
See this figure..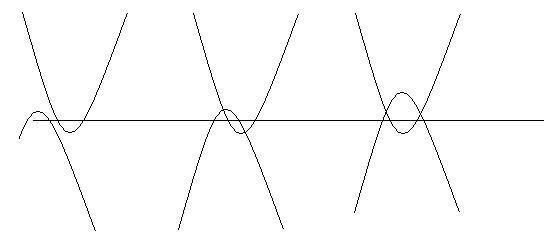
U need to take these cases...
And try them ..
I am sure u will get the answer using these..
there will be many cases.. u will have to eliminate some!
I hope this helps?
but the graph of the lower polynomial should not touch the x axis because if it does the denominator fr some value of x will be 0 so the function will be undefined . graph should lie below the x axis . please explain a litlle more in detail.
Denominator unfortunately has to be zero (otherwise this will not be satisfied.)!
Basically u are correct.. but i think this question requires us to overlook that aspect.
Using these graphs... and limits and continuity.. we can get the necessary conditions :)
what if the question is this i have edited the question slightly pls check.
this does not make much sense..
all u needed to say is that there exists a funciton..
f(x)=(px2 +6x-8)/(p+6x-8x2)
which is onto R
but the basic method will be the same..
atleast i cant think of any other way right now!