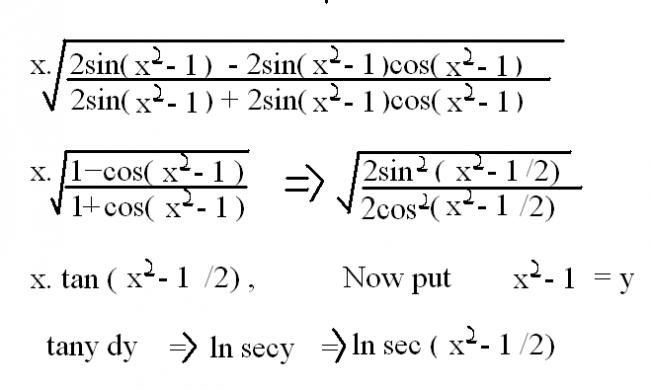Ans 2 ...first write x2 - 1 = t ... xdx = dt/2
so the integration reduces to \frac{1}{2}\int \sqrt{\frac{2sint - sin2t}{2sint +sin2t}} dt = \frac{1}{2}\int \sqrt{\frac{1-cost}{1+cost}}dt = \frac{1}{2}\int \frac{1-cost}{sint}dt
2.
3.
integrate w.r.t . alpha( α)
thnks gov bhai
FAR PRAACTIZE
-
UP 0 DOWN 0 0 7

7 Answers
Tapas Gandhi
·2010-03-15 03:50:36
e^{y}-1=t^{2}
e^{y}dy=2tdt \: but, \: e^{y}=1+t^{2}
\frac{2tdt}{(1+t^{2})t}
hence,
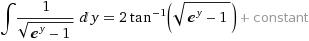
govind
·2010-03-15 03:52:04
Substitute e^{y} = t
\frac{dt}{dy} = t
So the integral reduces to
\int \frac{dt}{t\sqrt{t-1}} = 2\int \frac{dz}{z^{2}+1} = 2tan^{-1}\sqrt{e^{y}-1} + c
where z^{2} = t - 1
govind
·2010-03-15 04:00:59
qwerty
·2010-03-15 05:05:59
SR also has solved these problems already , u guys also know how to solve them , then why wasting time on same topic again and again ??????
Manmay kumar Mohanty
·2010-03-15 06:13:00
but it will help others like mee. yaar . post karne nein koi burai nahin.