1actually in the first question we need to find the sum of digits of
(k=0 to 2009) Σ g(x)
and thanks for the soln
integer type:::::
1) let f(x)=k/2009 and g(x)= f4(k)
(1-f(k))4 + (f(k))4
then sum of digits in the value of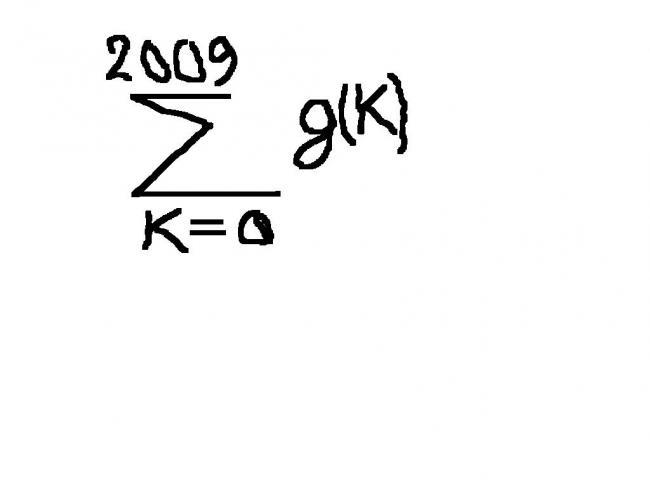 
is
2)
if S=1/2+1/6(12+22)+1/12(12+22+32)+.............+
1/3660(12+22+32+................602)
then sum of digits of S is
-
UP 0 DOWN 0 0 6
6 Answers
2622) Tr = (1 to r) Σ i2r(r+1) = r(r+1)(2r+1)6*r(r+1) = (2r+1)/6
S = ΣTr = n(n+1) +n6
now n=60
S = 620
sum of digits = 8
1) cant understand nor see the the question.
1
1708\hspace{-16}$Here $\bf{f(x)=\frac{x}{2009}}$ and $\bf{g(x)=\frac{f^4(x)}{(1-f(x))^4+f^4(x)}}$\\\\\\ So $\bf{g(x)=\frac{x^4}{(2009-x)^4+x^4}}$\\\\\\ So $\bf{g(k)=\frac{k^4}{(2009-k)^4+k^4}.......................(1)}$\\\\\\ $\bf{g(2009-k)=\frac{(2009-k)^4}{k^4+(2009-k)^4}................(2)}$\\\\\\ Adding $\bf{(1)+(2)}\;\;,$ We Get\\\\\\ $\bf{g(k)+g(2009-k)=1}$\\\\\\ So $\bf{\sum_{k=0}^{2009}g(k)=g(0)+g(1)+g(2)+..........+g(2009)=\frac{2009+1}{2}=1005}$\\\\\\ Using The Facts $\bf{g(k)+g(1-k)=1}$\\\\\\ So Sum of Digit in $\bf{\sum_{k=0}^{2009}=1+0+0+5=6}$