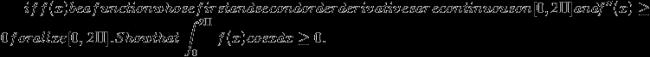Please do this one

[9][4]

Can u type the question??

I'll latexify it.

The qsn:- From ISI - Let f(x) be a continuous function whose first and 2nd derivatives are continuous in [0,2π] and f''(x)≥0 for all xin the given interval.

Show that \int_{0}^{2\pi }{f(x)cosxdx\ge 0 }.

Solution

f'(x)-f'(0)\ge 0

So \int_{0}^{x}{f'(x)dx}\ge \int_{0}^{x}{f'(0)dx}

From which we have f(x)\ge xf'(0)+f(0)

Now f(x)cosxdx\ge xf'(0)cosxdx+f(0)cosxdx

Thus \int_{0}^{2\pi}{f(x)cosxdx} \ge \int_{0}^{2\pi}{xf'(0)cosxdx}+\int_{0}^{2\pi}{f(0)cosxdx}\ge 0.