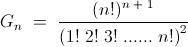
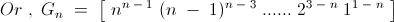
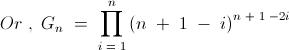
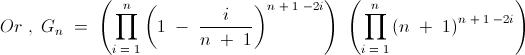
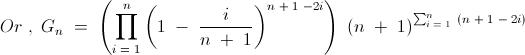
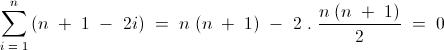
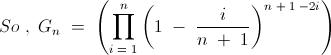
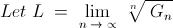
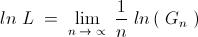
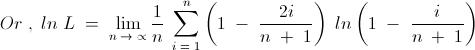
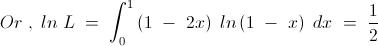
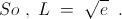
1) Prove:
\left|\begin{array}{cccc} 1+a_1 & 1 & \cdots & 1\\1 & 1+a_2 & \cdots & 1\\\vdots & \vdots & \ddots & \vdots \\1 & 1 & \cdots & 1+a_n\end{array}\right| = a_1a_2\cdots a_n \left(1+\dfrac{1}{a_1}+ \dfrac{1}{a_2}+\ldots + \dfrac{1}{a_n}\right)
(ai's are reals)
(2) Let f: R → R be a twice differentiable function, with positive second derivative. Prove that
f(x+f'(x)) ≥ f(x) for all real x.
3) Find all real solutions to the equation 4x + 6x2 = 5x + 5x2
4) For a>0, compute the integral
\int \dfrac{1}{x\sqrt{x^{2a}+x^a+1}}\ \mathrm dx,\quad x>0
5) For a positive integer n, compute the integral
\int \dfrac{x^n}{1+x+\frac{x^2}{2!}+\ldots + \frac{x^n}{n!}}\ \mathrm dx
6) For a positive integer n, let Gn denote the geometric mean of the binomial coefficients nCk for k = 0,1,2,..., n
Evaluate
\lim_{n\to\infty} \sqrt[n]{G_n}
kaymant sir i got a request to make...although still not doing great at these mean value theorems i feel a little bit confident with rolle's theorem but still i am very "LMVT-phobic"....so it is my sincere request if u could provide a few good "jee level"...problems based on new "objective" pattern it would be a great help in practice towards approaching jee in "calculus department" for the students.
thank you!
Those are right.
An alternative for 1):
Define
f(x)=\left|\begin{array}{cccc}x+a_1 & x & \cdots & x\\x & x+a_2 & \cdots & x\\ \vdots & \vdots & \ddots & \vdots \\x & x & \cdots & x+a_n\end{array}\right|
Prove by differentiating that f^{\prime\prime}(x)=0 and hence f must be a linear function and so one can write
f(x) = f(0) + f'(0)x
@kunl, Parampara ko aage badao. Ricky bhaiya ne tumhe LMVT padhaya ab tum mujhe thoda padha do!
1 > Given determinant : -
1 + a 1 1 1 ........................ 1
1 1 + a 2 1 ......................... 1
1 ................................................. 1
1 ................................................. 1
.
.
.
.
.
.
1 .............................................. 1 + an
Now , I ' ll take " a1 " common from the first column , " a2 " from the second column and so on .
= ( a1 a2 a3 ........... a n ) ........
:
: 1 + 1a1 1a2 1a3 ....................... 1an
:
: 1a1 1 + 1a2 1a3 ........................ 1an :
: 1a1 ................................................. 1an :
: .
: .
: .
: .
: .
: .
: 1a1 .............................................. 1 + 1an
:
:
........
Appplying " C1 → C1 + C2 + .................... Cn " ,
and , taking " 1 + 1a1 + 1a2 + ................... 1an " common from " C1 " , we get : -
= ........
:
: 1 1a2 1a3 ........................ 1an
:
: 1 1 + 1a2 1a3 ......................... 1an :
: 1 ................................................. 1an :
: .
: .
: .
: .
: .
: .
: 1 .............................................. 1 + 1an
:
........
Finally , " R2 → R2 - R1 " , " R3 → R3 - R1 " , ......................... " Rn → Rn - R1 " , gives us : -
= K ........
:
: 1 1a2 1a3 ........................ 1
:
: 0 1 0 .......................... 0 :
:
: 0 0 1 .......................... 0 :
: .
: .
: .
: .
: .
: .
: 0 ................................................ 1
:
........
= K ............................ ( expanding along " C 1 " )
Now , what is " K " ? Obviously : -
K = a1 a2 a3 ............. ( 1 + 1a1 + 1a2 + ............... 1an )
The reason why i said f'(x)f'(c) > 0 where c lies in between x and x+ f'(x)
case 1
x>0 f'(x) >0 obviously f'(c) >0
case 2
x<0 , f'(x)>0 obviously f'(c)>0
case 3
x>0 f'(x)<0 obviously f'(c)<0
x<0 ,f'(x)<0 obviously f'(c)<0
We have : -
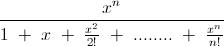
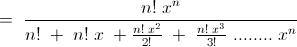
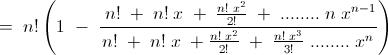
Now , the given integral : -
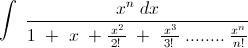
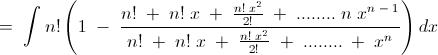
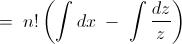
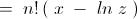
Note : - In this post , as well as my first post , I ' ve omitted the constant of integration .
okies[1]
btw are u not watching the math...sorry for late reply was too much engrossed into it!
That is exactly my point : -
now lets "assume x is non-zero" then it is easy enought to observe that x=1 is the "only non-zero" number for which boths sides can be equal based on that t1 and t2 are distinct since they lie in different intervals namely(4,5) and (5,6).
This is based only upon observation .
i may not have been clear in my last post...coz i posted it in short asd i thought it is easily observable let me elaborate
(i) =(ii)
implies
x2t2x2-1=xt1x-1
now one way for the above to hold is x=0 when both sides become identically zero..
now lets "assume x is non-zero" then it is easy enought to observe that x=1 is the "only non-zero" number for which boths sides can be equal based on that t1 and t2 are distinct since they lie in different intervals namely(4,5) and (5,6).
and this also proves that no other root does exist!
now i hope m pretty clear!
@ricky tht i already mentioned in beginning of my post but graph can't be a substitute for a "rigorous proof"...n i hope u agree...so i used LMVT to prove that no solution other than 0,1 exists[1]
waise all credit goes to u...u are my mvt teacher [1]
3 >
Graphs say it all : -
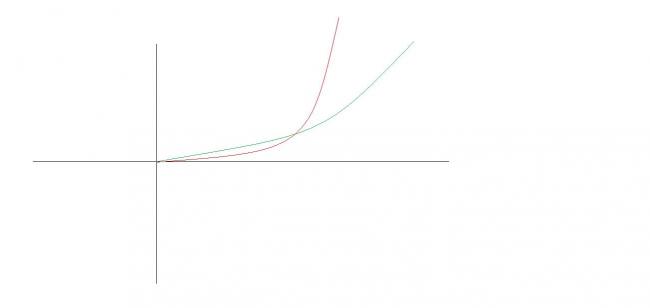
The red line : - y1 = 6 x2 - 5 x2
The blue line : - y2 = 5 x - 4 x
Since " y1 ≥ 0 " , so I have drawn " y2 " for positive " x " only .
3rd one seems easier to me
there is one obvious solution(infact two obvious :P 0 and 1...but most obvious one is 0..)
so observing that 0 is one solution obviously lets go for other solutions
lets create a function
treating x as a constant
h(t) =tx
now this satisfies the LMVTs hypothesis in [4,5]
so there exists a t1 such that xt1x-1=5x-4x.....(ii)
similary consider g(t)=tx2 on interval[5,6]
which gives t2 such that x2t2x2-1=6x2-5x2....(i)
now since (i) =(ii) and t2 and t1 are distinct since they lie in different intervals! therefore,we should have x=1 from(i)=(ii)
clearly x=0,1 satisfy the given equation!
3)
Not a complete solution
clearly x=0 is a solution , as the RHS and LHS both are increasing function on x, there can be at most one point of intersection , again we see x= 1 is a solution , for negative part ,let me think more ;(
2)
f(x + f'(x))- f(x)f'(x)= f'(c) x<c<x+ f'(x)
f(x + f'(x))- f(x) = f'(x)f'(c) >0 (because f' is an increasing function)
Sir , I would request you heartily not to give the solutions , or any kind of hints for these problems until at least the day after tomorrow , as I want really want to solve them on my own : )