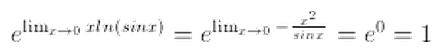problem in limits

Lt_xâ†’0Lt_{nâ†’âˆž}1n³âˆ«ⁿ_r=1[r² (sin x)^x] ,[x] is greatest integer fn² ;âˆ« is summation

2 Answers

please someone explain how to do this type of sum

262

Aditya Bhutra ·2011-06-23 03:20:45

x-1<[x]â‰¤x
hence
let sinx ^x =z
(r²z )-1 <[r² .z] â‰¤ r²z
taking summation on all sides,

(n(n+1)(2n+1)6 .z )- n < sum[r² .z] â‰¤ (n(n+1)(2n+1)6 .z )

taking limits , nâ†’âˆž

1.(1+1/n)(2+1/n)6 .z - 1/n² < sum[r² .z] <1.(1+1/n)(2+1/n)6 .z
therefore
z/3 < sum[r² .z] â‰¤ z/3
hence lim_{nâ†’âˆž} sum[r² .z] = z/3 = sinx ^x

now next part

lim_xâ†’0 sinx ^x =

√ √ || {} [] () → ~ ^ x x x → → ln log lg lim lim cos sin tan cot arcsin arccos arctan

∫ ∫ ∫ ∫ ∫ ∬ ∬ ∬ ∬ ∬ ∭ ∭ ∭ ∭ ∭ ⨌ ⨌ ⨌ ⨌ ⨌

∑ ∑ ∑ ∑ ∑ ∮ ∮ ∮ ∮ ∮ ∏ ∏ ∏ ∏ ∏ ∐ ∐ ∐ ∐ ∐

+ - × ÷ ± ∓ = ∪ ∩ ≠ ∼ ≈ ∅ ∀ ∃ ∈ ∋ ∝ ≤ ≥ ≃ ≅ ≡ < > ≪ ≫ ⊂ ∉ ⊃ ⊆ ⊇ ⇒ ⇐ ⇔ ⇒ ⇐ ⇔ ⇑ ⇓ ⇕ → ← ↔ → ← ↔ ↑ ↓ ↕ ↖ ↗ ↘ ↙ ↪ ↩ ⇀ ↼ ⇁ ↽

° ∂ ∞ α β γ δ θ λ μ ν ξ π ρ σ φ ω ε ƒ κ τ υ Γ Δ Λ Σ Π Ω