IS IT NOT OBVIOUS?
This is crackable but nice:
f:(a,b) \rightarrow \mathbb{R} is continuous. Prove that given x_1, x_2, x_3,...,x_n in (a,b), there exists x_0 \in (a,b) such
that f(x_0) =\frac{1}{n} \left(f(x_1)+f(x_2)+f(x_3)+...+f(x_n) \right)
-
UP 0 DOWN 0 0 7

7 Answers
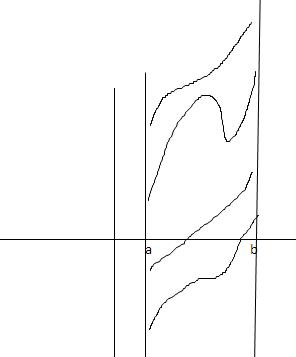
f(x0) = 1/n[f(x1)+f(x2)+.................f(xn)]
is the arithematic mean of [f(x1)+f(x2)+.................f(xn)]
And an Arithematic Mean always lies in between the maximum and minimum value
ie. x0 belongs to (a,b)
THAT'S WHY I SAID IT IS OBVIOUS.
IS THERE SOMETHING ELSE IN QUESTION? WHICH I AM NOT UNDERSTANDING.
I repeat a famous quote that a prof once told
"What is obvious to you might not be obvious to me"
Is it so obvious. Probably, one should remember that the Intermediate value property holds for closed intervals.
In other words the IMV is being applied to the interval ________ ?