Question is based on Area under curve.

In the first quadrant x≥0, y≥0, so the graph is simply y = |x² - 4x| which is basically the parabola x² - 4x with the part lying below the x axis reflected up.

In the second quadrant, x<0, y≥0, so the graph is y = |x² + 4x|

In the third quadrant, x<0, y<0, so the graph is -y = |x² + 4x| i.e. y=-|x² + 4x|.

And in the fourth quadrant, x≥0, y<0, so the graph is -y = |x² - 4x| i.e. y = -|x² - 4x|.

Hence, the required graph is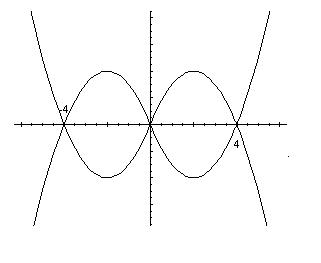

So the required area is 4 times
\int_0^4 (4x-x^2)\ \mathrm dx
i.e 4 323 = 1283

The number of tangents is obviously 4 which could be drawn from (8,0).

I think aakash has made a mistake by giving ans as ACD

How can you have "maybe 3 tangents" when exactly 4 are possible?