tax ya tan? lol.
Write it as -:
y = \frac{2sin(x + \Pi/12)cos(x - \Pi/12)}{2cos(x + \Pi/12)sin(x - \Pi/12)} = \frac{sin(2x + \Pi/6)}{sin(2x - \Pi/6)}
The domain of this function is x \epsilon (R - {\Pi/12})
Now we must find the increasing-decreasing sections of the domain.
To do this, we find maxima/minima points in the domain.
f'(x) = \frac{2sin(2x - \Pi/6)cos(2x + \Pi/6) - 2sin(2x + \Pi/6)cos(2x - \Pi/6)}{sin^2(2x - \Pi/6)} = \frac{sin(4x - \Pi/3) - sin(4x + \Pi/3)}{sin^2(2x - \Pi/6)} = \frac{2sin(-\Pi/3)cos(4x)}{sin^2(2x - \Pi/6)}
Now for f'(x) to be 0, cos(4x) = 0 => 4x = npi/2 = x = npi/8 where n = odd integer.
So if we restrict our domain to [0, 2pi], x = pi/8, 3pi/8, 5pi/8, 7pi/8, 9pi/8, 11pi/8, 13pi/8, 15pi/8 are the eight points across which we obtain changes in sign of f'(x).
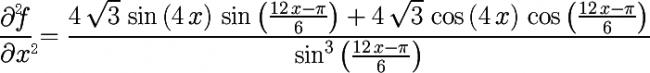
If we put x = pi/8 in f"(x), we obtain a positive value. Hence it is a point of minima. Accordingly all points are min, max, min, max, min, max, min, max.
So f(x) decreases from 0 to pi/8, increases from pi/8 to 3pi/8 and so on....
Hence you can divide sections of the domain [0, 2pi] into [0 to pi/8] U [pi/8, 3pi/8] etc.
So as x ε [0, pi/8] U [pi/8, 3pi/8] U ......
f(x) ε [f(pi/8), f(0)] U [f(pi/8), f(3pi/8)] U ......
Notice how I've switched places of pi/8 and 0 in first bracket when I apply f(x). This is because the function is monotonically decreasing in that section of the domain. Hence it will take min value and give max value, and vice versa. The next bracket has normal order instead of switching because f(x) increases there.
I assumed [0, 2pi] to be our restricted domain where f(x) is undefined at x = pi/12.
The f(x) ε part is the range and x ε part is sections of domain.
(Hope I've calculated correctly)