39huh!!
editing :x
1) Let R be a relation on N defined by x + 2y = 8. The domain of R is
(a) {2,4,8} (b) {2,4,6,8) (c){2,4,6} (d) {1,2,3,4) . Give the reason to your answer.
2)The relation 'R' in NxN such that (a,b) R(c,d) <==> a+d=b+c. How this can be the equivalence relation?
b)Modulus Function
if a, b are positive real numbers,then
x2 ≥ a2 <=> lxl ≥ a <=> x ≤ (-a) or x ≥ a.
HOW x ≤ (-a) ?
4) Greatest Integer Function
[x] > k => x ≥ k + 1, where k is an integer. Please prove this with some example, am not able to understand this property.
5)Smallest integer function.
(-x) = -(x) + 1, where x belongs to R-Z, prove this with some example.
I am not able to make the bracket which are used to represent smallest integer functions, so I made usage of open bracket.
-
UP 0 DOWN 0 0 9
9 Answers
393)
x2≥a2
implies |x|≥a
implies x≥a or -x≥a
-x≥a
multiplying through out by minus sign , the sign of inequality also changes
making it x≤(-a)
11Ohh got it Kira (bada ajeeb naam hai [3][3])
thanks and what is edited here?[3]
39Q1. As R is a relation defined on natural numbers, we have to provide some natural x such that y is also natural.
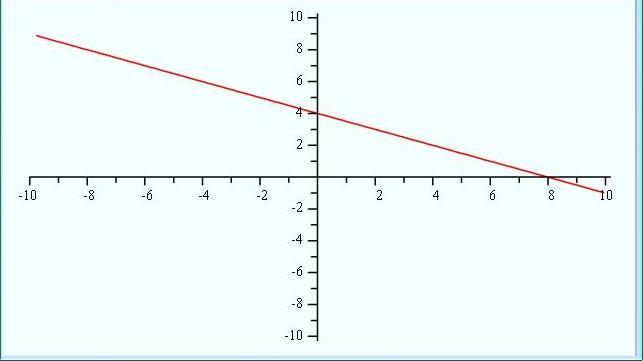
Natural x such that y is also natural would be even, due to the division by 2. They are -: 2, 4, 6. If we put x = 8, we get y = 0, which is not natural.
Q2. To prove that it is an equivalence relation,
Reflexivity
(a, b) R (a, b) => a + b = a + b. This relation holds (pretty obvious) and R is reflexive.
Symmetry
(a, b) R (b, a) => a + b = b + a. This relation holds due to commutative law of addition. Hence R is symmetric.
Transitivity
We have (a, b) R (c, d) => a + b = c + d.
And (c, d) R (e, f) => c + d = e + f
Then we should have (a, b) R (e, f) as a valid relation.
(a, b) R (e, f) => a + b = e + f must be proved.
Now as a + b = c + d and c + d = e + f, a + b = e + f.
Hence (a, b) R (e, f) holds. Hence R is transitive.
So R is an equivalence relation.
Q4. [x] > k implies [x] ≥ k + 1 where k is an integer.
Let x be 3.6 and k be 1.
Obviously [3.6] > 1.
This also implies [3.6] ≥ 2 which is true as 3 > 2.
Try k = 2.
[3.6] > 2
=> [3.6] ≥ 3 which is true as 3 = 3.
Now let's try negative integers.
Let x = -2.2 and k be -4.
[-2.2] > -4
=> [-2.2] ≥ -5 which is true.
And so on..
1about the first part y=(8-x)/2................ so the function is from real to natural................... so 8-x/2 should be an integer... so domain is
(2,4,6). am i right...........................................
1prithis good post.... all your problems are very conceptual.... keep going post..............