for Q1 i dont think we can predict accurately.......but yes atleast one root of g"'(x) will be there becoz g"(a)=g"(b)=0[1]
g(x)=0∫x f(t)dt ,g"(x) is continuous and differentiable.
a<c<b
g"(a)=0;g"(b)=0;g"(c)=0
Also g'(a)=0 ,g'(b)<0
Q1. g"'(x) has in [a,b] exactly
A)2 real roots
B)1 real root
C)no real root
D)3 real roots
Q2.f(x) has in [a,b]
A)atleast 2 real roots
B)exactly 1 real root
C)exactly 2 real roots
D)none of these
-
UP 0 DOWN 0 0 11

11 Answers
yaar yeh to assan hai
g`(x)=f(x)
so take a new function g`(x) as h(x) and u have mentioned the conditions for h(x) to follow ROLLE THEOREM
q1) g'''(x)=f''(x)
but f'(a)=f'(b)=f'(c)=0
but a<c<b.
therefore the f''(x) shud have two roots.
q2)g'(x)=f(x)
but g'(a)=0 therefore it is one of the root.
and also combining g'(b)< 0,g''(c)=g''(b)=0 we can conclude dat there is other root in the interval [c,b]
hey sankara.in q1 it is asked in [a,b] not in [a,c].......as u have taken in post#9......[1][1]
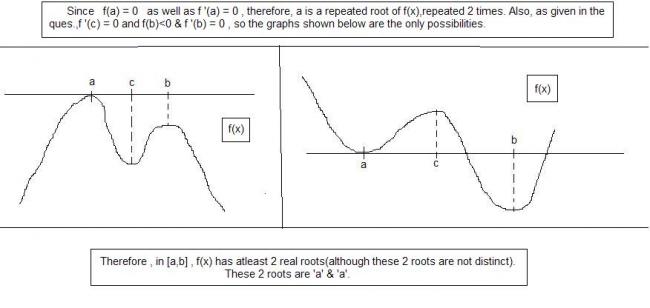
Q 1)
g''(a) = g''(c) = 0 & g''(c) = g''(b) = 0
Hence applying Rolles Thrm. , we can say that
g'''(x) has atleast 1 real root in [a,c] and atleast 1 real root in [c,b]
Hence g'''(x) has atleast 2 real roots in [a,b].
So from the given options , by eliminating B),C) & D) we can say that in [a,b] g'''(x) has exactly 2 real roots. BUT if the same question had options like
in [a,b], g'''(x) has
(A)atleast 2 real roots
(B)at most 2 real roots
(C)exactly 2 real roots
(D)atleast 2 roots,not necessarily real
I do not know which option to mark.[2][2][2]