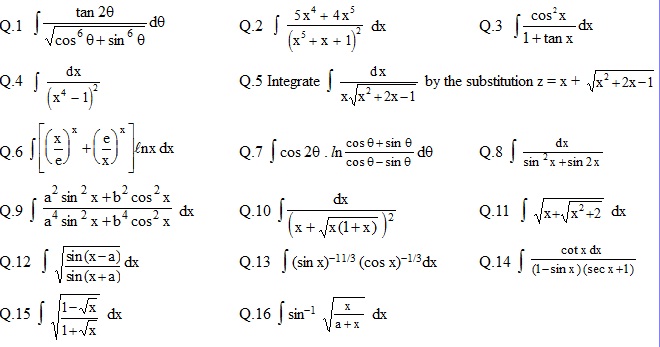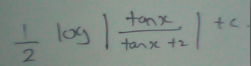1708\hspace{-16}\bf{(2):: \int\frac{(5x^4+4x^5)}{(x^5+x+1)^2}dx}$\\\\\\ $\bf{\Rightarrow \int\frac{(5x^4+4x^5)}{x^{10}.(1+x^{-4}+x^{-5})^2}dx}$\\\\\\ $\bf{\Rightarrow \int\frac{\left(5x^{-6}+4x^{-5}\right)}{\left(1+x^{-4}+x^{-5}\right)^2}dx}$\\\\\\ Now Let $\bf{\left(5x^{-6}+4x^{-5}\right)=t}$\\\\\\ Then $\bf{\left(5x^{-6}+4x^{-5}\right)=-dt}$\\\\\\ So $\bf{= -\int \frac{1}{t^2}dt = \frac{1}{t}+\mathbb{C}}$\\\\\\ $\bf{=\frac{1}{1+x^{-4}+x^{-5}}+\mathbb{C}}$\\\\\\ $\bf{=\frac{x^5}{x^5+x+1}+\mathbb{C}}$
230515.\int\sqrt{\frac{1-\sqrt{x}}{1+\sqrt{x}}}dx=\int\frac{1-\sqrt{x}}{\sqrt{1-x}}dx
Let sin2θ = x
\int\frac{1-\sin\theta}{\cos\theta}2\sin\theta \cos\theta d\theta
= 2\int\sin\theta d\theta-2\int\sin^{2}\theta d\theta
=-2\cos\theta-2\int\frac{1-\cos 2\theta}{2}d\theta
=-2\cos\theta - \theta + \frac{\sin 2\theta}{2}+C
= -2\sqrt{1-x}-\sin^{-1}\sqrt{x}+\frac{\sqrt{x}\sqrt{1-x}}{2}+C
1708\hspace{-16}\bf{(6)\;\; \int \left(\left(\frac{x}{e}\right)^x+\left(\frac{e}{x}\right)^x\right)\cdot \ln (x)dx}$\\\\\\ Let $\bf{\left(\left(\frac{x}{e}\right)^x-\left(\frac{e}{x}\right)^x\right)=t\;\;,}$ Then \\\\\\ $\bf{\left(\left(\frac{x}{e}\right)^x+\left(\frac{e}{x}\right)^x\right)\cdot \ln(x)dx=dt}$\\\\\\ So Integration is $\bf{\int 1\cdot dt = t+\mathbb{C}}$\\\\\\ So $\bf{\int \left(\left(\frac{x}{e}\right)^x+\left(\frac{e}{x}\right)^x\right)\cdot \ln (x)dx=\left(\left(\frac{x}{e}\right)^x-\left(\frac{e}{x}\right)^x\right)+\mathbb{C}}$
13each and every book i look into i get the 15 number sum ......sir u have even given it in shastras..can u plzzz given the solution ?
1Take x= cos2θ
thn its coming - log( cosθ)
Sustitute for θ nd u get the ans...
Divyans Jhunjhunwala For ques 15
158For 12,..
-cosa.sin-1(cos xcos a)-sina.log|sin x-√sin2x-sin2a|+C
??
230513)\int \sin^{-11/3}x\cdot\cos^{-1/3}xdx
=\int \tan^{-11/3}x\cdot \sec^{4}xdx
=\int \tan^{-11/3}x(1+\tan^{2}x)\text{ d}\tan x
=-\frac{3}{8}\tan^{-8/3}-\frac{3}{2}\tan^{-2/3}x+C
1708\hspace{-16}\bf{(11)\;\int\sqrt{x+\sqrt{x^2+2}}\; dx}$\\\\\\ Let $\bf{\boxed{\bf{\left(x+\sqrt{x^2+2}\right)=t^2}}\Leftrightarrow \left(1+\frac{1}{2\sqrt{x^2+2}}.2x\right)dx = 2tdt}$\\\\\\ $\bf{\left(\frac{x+\sqrt{x^2+2}}{\sqrt{x^2+2}}\right)dx =2tdt\Leftrightarrow dx = \frac{2\cdot \sqrt{x^2+2}}{t}dt}$\\\\\\ Now using $\bf{\left(\sqrt{x^2+2}+x\right)\cdot\left(\sqrt{x^2+2}-x\right)=2}$\\\\\\ $\bf{t^2\cdot\left(\sqrt{x^2+2}-x\right)=2\Leftrightarrow \boxed{\bf{\left(\sqrt{x^2+2}-x\right)=\frac{2}{t^2}}}}$\\\\\\ So $\bf{\sqrt{x^2+2}=\frac{1}{2}\cdot \left(t^2+\frac{2}{t^2}\right) = \frac{1}{2}\cdot \left(\frac{t^4+2}{t^2}\right)}$\\\\\\ So Integration is $\bf{\int t\cdot \frac{\left(t^4+2\right)}{t^2}.\frac{1}{t}dt}$\\\\\\ So $\bf{\int \left(\frac{t^4+2}{t^2}\right)dt = \int t^2dt+2\cdot \int t^{-2}dt }$\\\\\\ So $\bf{=\frac{1}{3}\cdot t^3 -\frac{2}{t}+\mathbb{C}}$\\\\\\
\hspace{-16}$So $\bf{=\frac{1}{3}\cdot \left(x+\sqrt{x^2+2}\right)^{\frac{3}{2}}-2\cdot \left(x+\sqrt{x^2+2}\right)^{-\frac{1}{2}}+\mathbb{C}}$\\\\\\ $\bf{\bullet }$Alternatively..........\\\\\\ Using $\bf{\left(x+\sqrt{x^2+2}\right)=e^{2t}\;\;, }$ Then $\bf{\left(\sqrt{x^2+2}-x\right)=2\cdot e^{-2t}}$\\\\\\ Integral convert into $\bf{\int e^t \cdot \left(e^{2t}+2e^{-2t}\right)dt}$
1708\hspace{-16}\bf{(9)\;\; \int\frac{a^2\sin^2 x+b^2\cos^2 x}{a^4\sin^2 x+b^4\cos^2 x}dx}$\\\\\\ Divide both $\bf{N_{r}}$ and $\bf{D_{r}}$ by $\bf{\cos^2 x}$ \\\\\\ $\bf{\int\frac{a^2\tan^2 x+b^2}{a^4\tan^2 x+b^4}dx = \frac{1}{a^4}\int \frac{\tan^2 x+\left(\frac{b}{a}\right)^2}{\tan^2 x+\left(\frac{b}{a}\right)^4}dx}$\\\\\\ Now Put $\bf{\left(\frac{b}{a}\right)=d}$ and $\bf{\tan x=t \Leftrightarrow \sec^2 xdx =dt}$\\\\\\ $\bf{dx=\frac{1}{(1+t^2)}dt}$\\\\\\ So Integral is $\bf{\frac{1}{a^4}\int\frac{t^2+d}{(t^2+d^2)\cdot (1+t^2)}dt}$\\\\\\ Now Using Partial fraction \\\\\\ $\bf{=\frac{1}{a^4\cdot(d+1)}\left(\int \frac{d}{(t^2+d^2)}dt+\int\frac{1}{(t^2+1)}dt\right)}$\\\\\\ $\bf{=\frac{1}{a^4}\cdot \tan^{-1}\left(\frac{t}{d}\right)+\frac{1}{a^4\cdot (d+1)}\cdot \tan^{-1}(t)+\mathbb{C}}$\\\\\\ So $\bf{\int\frac{a^2\sin^2 x+b^2\cos^2 x}{a^4\sin^2 x+b^4\cos^2 x}dx=\frac{1}{a^4}\cdot \tan^{-1}\left(\frac{\tan x}{d}\right)+\frac{1}{a^4\cdot (d+1)}\cdot \tan^{-1}(\tan x)+\mathbb{C}}$ \\\\\\
2305\int\frac{\tan 2\theta\,d\theta}{\sqrt{\sin^4\theta+\cos^4\theta-\cos^2\theta\sin^2\theta}}
=\int \frac{\frac{2\tan\theta}{1-\tan^2\theta}\cdot \sec^2\theta\,d\theta}{\sqrt{\tan^4\theta+1-\tan^2\theta}}
Substituting tan2θ=z,
I=\int\frac{dz}{(1-z)\sqrt{z^2+1-z}}
Substituting 1-z=1t,
I=\int \frac{\frac{1}{t^2}\,dt}{\frac{1}{t}\sqrt{(1-\frac{1}{t})^2+1-(1-\frac{1}{t})}}
=\int \frac{dt}{\sqrt{t^2-1+t}}
=\int\frac{dt}{\sqrt{(t-\frac{1}{2})^2-\frac{5}{4}}}
=\frac{1}{\sqrt{5}}\ln|t-\frac{1}{2}+\sqrt{t^2-1+t}|+C
Shaswata Roy Answer for question 1.
