If A+B+C=Pi , then prove that cos A+cos B+ cos C<3/2, where A, B, C are distinct.
solve using graph
62Jensen's inequality will help.. (but there is a small issue there wchih i think can be sorted out.... )
http://en.wikipedia.org/wiki/Jensen%27s_inequality
11Using Jenson's Inequality ,
If f(x) is such that f '(x) > 0 and f '' (x) < 0 , then
f (m x2 + n x1m+n) ≥ n f(x1) + m f(x2)m+n
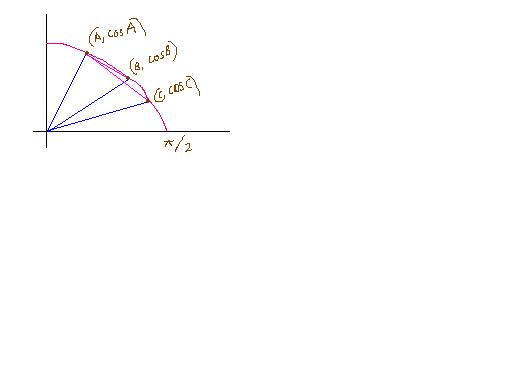
We get,
cos ( A + B +C3 ) > cos A + cos B + cos C3
Therefore, 1/2 > cos A + cos B + cos C3
Thus,
cos A+cos B+ cos C<3/2 [Given A+ B+ C = pie]
Hence Proved [1]
62Tushar this can be proved only if each of A, B and C are less than pi/2
which is infact not given!
so you will have to prove this as well
11But sir the equality holds only when A= B= C = pie/3
cos A = cos B = cos C = pie/3 and A + B+ C =pie
or A = pie/3
1what is thios jenson's inequality
i didnt get it
can sum1 explain it in details
