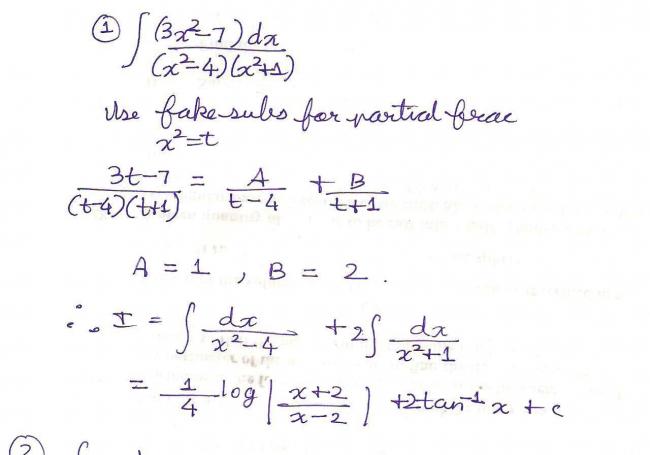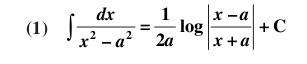39
evaluate !!!!!!!!!!!!!!
1.
\int \frac{3x ^2 - 7 dx}{ (x^2 -4) ( x^2 + 1 ) }
2 .
\int \frac{ dx}{ x.\sqrt{x^6 + 1} }
3.
\int \frac{ \sqrt{x} dx}{(1+ x^2)^{\frac{7}{4}}}
just practice problems [1]
-
UP 0 DOWN 0 1 11
11 Answers
21for 3rd one substitute \sqrt{x}=z
so we get integral of form 2\int z^2(1+z^4)^{-7/4}dz
now substitute t=\left(1+z^{-4} \right)^{\frac{1}{4}}
this is analogous to integral of form \int x^m(a+bx^n)^pdx
if \left(\frac{m+1}{n}+P \right) is an integer and P is a fraction we put a+bx^n=t^kx^n wer k is deno of fraction P
12nd one
-\int \frac{x^3.dx}{-x^7\left(1+\frac{1}{x^6} \right)^{\frac{1}{2}}} \\ \text{apply parts}\\ -I=2x^3\sqrt{1+\frac{1}{x^6}}-6\underline{\int \left(\frac{\sqrt{1+x^6}}{x} \right)}+C\\ \\ \text{evaluating underlined part}\\ {1+x^6}=z^2\Rightarrow \frac{2z.dz}{6x^5}=dx\\ \int \frac{2z^2.dz}{6(z^2-1)}\text{this can be evaluated easily }
21for second one
this integral \int x^{-1}(x^6+1)^{-\frac{1}{2}}dx
is analogous to integral of form \int x^m(a+bx^n)^pdx
if \frac{m+1}{n} is an integer and P is a fraction put (a+bx^n)=t^k wer k is teh deno of fraction P
so substitute (1+x^6)^{\frac{1}{2}}=t
1thanks everyone for solution
prophet sir ---> thanks a lot for using substitution to 3rd ques .....
plz everyone try this
!!! any other way to solve the ques --2 and- --3-- !!!!1
at the end i will post my solution
29Omkar....these question seems to be from Brilliant YG files..
in the second one substitute x^{3} = t
3x^{2}dx = dt
then u will get \frac{1}{3}\int \frac{dt}{t\sqrt{t^{2}+1}}
then substitue t^{2}+1=z^{2}
tdt = zdz
then u will get
1/3*\int \frac{dz}{z^{2}-1}
which can be easily integrated now using the formula
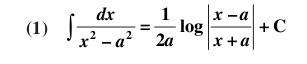
12. ∫dx/(x4√(1+x-6)) or ∫x-4dx/√(1+(x-3)2) now take x-3=z .....
1yaa govind bhai
\int \frac{dx}{x.\sqrt{x^ 6 + 1}}
let x6+ 1 = t2
6 x5dx = 2.t .dt
dx = t dt 3. x 5
integral reduces to
\int \frac{dt}{x^ 6}
\int \frac{dt}{t^2 - 1} = \frac{1}{3} log\frac{\sqrt{x^ 6 + 1 }-1}{\sqrt{x^ 6 + 1}+ 1 } + c
anyone trying three with a simpler method than eragon
23Q3> put \; x=t^{2}
\Rightarrow\; I=\int \frac{2t^{2}dt}{(1+t^{4})^{\frac{7}{4}}}
take t4 common from deno from d bracket
\Rightarrow\; I=\int \frac{2t^{2}dt}{t^{7}(\frac{1}{t^{4}}+1)^{\frac{7}{4}}}
\Rightarrow\; I=\int \frac{2t^{-5}dt}{(\frac{1}{t^{4}}+1)^{\frac{7}{4}}}
now take (\frac{1}{t^{4}}+1)=m, -4t^{-5}dt=dm
\Rightarrow\; I=-\int \frac{dm}{2m^{\frac{7}{4}}}