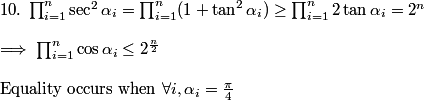
 Shaswata Roy Nice solution :)Upvote·0· Reply ·2013-10-30 22:52:15
Shaswata Roy Nice solution :)Upvote·0· Reply ·2013-10-30 22:52:15
\text{1)Evaluate:}
a)\lim_{n\rightarrow \infty}\frac{1}{2n}\log\binom{2n}{n}
b)\lim_{n\rightarrow \infty}\left[\frac{1}{a+n}+\frac{1}{2a+n}+\cdots +\frac{1}{na+n}\right]
\text{2)Let } a_{1}=1 \text{ and }a_{n}=n(a_{n-1}+1)\ \forall n\geq 2 .\text{Find }
\lim_{n\rightarrow \infty}\left(1+\frac{1}{a_{1}}\right)\left(1+\frac{1}{a_{2}}\right)\cdots \left(1+\frac{1}{a_{n}}\right)
\text{3)Let }a_0 =0<a_1<a_2<\cdots <a_n \text{ be real numbers.}
\text{Suppose }p(t)\text{ is a real valued polynomial of degree n such that}
\int\limits^{a_{j+1}}_{a_{j}}p(t)\, dt=0 \qquad \text{ for all } 0\leq j \leq n-1
\text{Show that for }0\leq j\leq n-1 \text{ the polynomian p(t)has }
\text{exactly one root in the interval }(a_j,a_{j+1})
\text{4)Let f(u) be a continuos function and,let \[u\]}\rightarrow GIF
\text{Show that for any }x>1
\int \limits ^{x}_{1}\[u\](\[u\]+1)f(u)\, du=2\sum\limits ^{\[x\]}_{i=1}i\int \limits^{x}_{i}f(u)\, du
\text{5)Let f(x) be a function differentiable n+1 times for some }n>0
f(1)=f(0)=f^{(0)}(0)=\cdots =f^{(n)}(0)=0
\text{Prove that }f^{(n+1)}(x)=0 \text{ for some }x\in (0,1)
\text{6)Prove that for }n>0:
\int \limits ^{\pi/2}_{0}\frac{\sin(2n+1)x}{\sin x}\, dx=\frac{\pi}{2}
\text{7)Show that}
\int \limits^{\pi}_{0}\left|\frac{\sin nx}{x}\right|\, dx \geq \frac{2}{\pi}\left(1+\frac{1}{2}+\cdots +\frac{1}{n}\right)
\text{8)Using the identity }\log x = \int^x_1\frac{dt}{t}\qquad x>0 \text{ ,show that for }n\geq 1
\frac{1}{n+1}\leq \log\left(1+\frac{1}{n}\right)\leq \frac{1}{n}
\text{9)Let }a_1>a_2>a_3\cdots >a_r>0
\text{Compute }\lim_{n \rightarrow \infty}(a_1^n+a_2^n+\cdots +a_r^n)^{1/n}
\text{10)Find the maximum value of }\cos\alpha_1\cdot\cos\alpha_2\cdots \cos \alpha_n
\text{under the restriction }0\leq \alpha_1,\alpha_2,\cdots ,\alpha_n\leq \frac{\pi}{2} \text{ and }}
\cot\alpha_1\cdot\cot\alpha_2\cdots \cot \alpha_n =1.
\hspace{-16}(6)\;\; $Let $\bf{I_{2k+1} = \int_{0}^{\frac{\pi}{2}}\frac{\sin (2k+1)x}{\sin x}dx.........(1)}$\\\\\\ Replace $\bf{k\rightarrow (k+1)}$\\\\\\ $\bf{I_{2k+3} = \int_{0}^{\frac{\pi}{2}}\frac{\sin (2k+3)x}{\sin x}dx................(2)}$\\\\\\ So $\bf{I_{2k+3}-I_{2k+1} = \int_{0}^{\frac{\pi}{2}}\frac{\sin (2k+3)x-\sin (2k+1)x}{\sin x}dx}$\\\\\\ So $\bf{I_{2k+3}-I_{2k+1} = \int_{0}^{\frac{\pi}{2}}\frac{2\cos (2k+2)x\cdot \sin x}{\sin x}dx =0}$\\\\\\ So $\bf{I_{2k+3} = I_{2k+1}.}$\\\\\\ Now Replace $\bf{k\rightarrow (k-1)}$\\\\\\ $\bf{I_{2k+1} = I_{2k-1}}$\\\\\\ Using Recursively, We Get\\\\\\ $\bf{I_{2k+3} = I_{2k+1} = I_{2k-1}=I_{2k-3}=........=I_{3}}$\\\\\\ Now $\bf{I_{1} = \int_{0}^{\pi}\frac{\sin (2\cdot 1+1)}{\sin x}dx = \int_{0}^{\frac{\pi}{2}}\frac{3\sin x -4\sin ^3 x}{\sin x}=\frac{\pi}{2}}$\\\\\\
\hspace{-16}$So $\bf{I_{2k+3} = I_{2k+1} = I_{2k-1}=I_{2k-3}=........=I_{3} =\frac{\pi}{2}}$\\\\\\So $\bf{I_{2k+1}=\int_{0}^{\frac{\pi}{2}}\frac{\sin (2k+1)x}{\sin x}dx = \frac{\pi}{2}}$
8.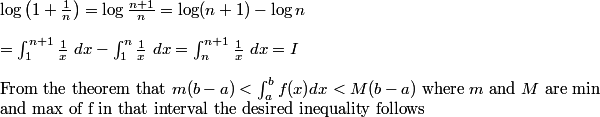
I got some answers...
1) a - log2
1) b - log(1+a)a
2) 5/2
9) a1
an+1(n+1)!=ann!+1n!
Which gives
an+1(n+1)!=1+1+1/2!+1/3!+...+1/n!
this might help
For no. 4, expand both the LHS and RHS into integrals between successive integers. Then try to rearrange the terms of the RHS to get the LHS.
Sorry Soumya I had been typing that out for a long time I didnt know you had posted this.