1057actually the answer given for 2nd question is 8.I was also getting the same answer.so it's a misprint right.?
1)If \dpi{100} \fn_jvn \int_{a}^{b}(2+x-x^{2}) is maximum find a+b?
2)For f(x)=61+31ex the possible number of different integral values which f(x) can take is?
3)if \dpi{100} \fn_jvn \lim_{x\rightarrow \infty }\sqrt[3]{8x^{3}+mx^{2}}-nx =1
find m+n?
-
UP 0 DOWN 0 0 4
4 Answers
1708(1)
\hspace{-16}$So from graph Area is Maximum when $\bf{a=-1}$ and $\bf{b=2}$
(2)
\hspace{-16}$Here $\bf{f(x)=\frac{6}{1+31e^x}\; \forall x\in \mathbb{R}}$\\\\\\ Now $\bf{\lim_{x\rightarrow -\infty}f(x)=\lim_{x\rightarrow -\infty}\frac{6}{1+31e^x}\rightarrow 6}$\\\\\\ and $\bf{\lim_{x\rightarrow +\infty}f(x)=\lim_{x\rightarrow +\infty}\frac{6}{1+31e^x}\rightarrow 0}$\\\\\\ and $\bf{f(x)}$ is a Cont. function. So $\bf{f(x)\in \left\{1,2,3,4,5\right\}}$\\\\\\ So Total $\bf{5}$ distinct values of $\bf{f(x)}$ exists.
(3)
\hspace{-16}$Given $\bf{\lim_{x\rightarrow \infty}\sqrt[3]{\bf{8x^3+mx^2}}-nx = 1}$\\\\\\ Now put $\bf{x=\frac{1}{y}}$ and $\bf{y\rightarrow \infty}$\\\\\\ $\bf{\lim_{y\rightarrow 0}\frac{(8+my)^{\frac{1}{3}}-n}{y}=1}$\\\\\\ Now for the existance of limit, Limit must be $\bf{\frac{0}{0}-}$ form.\\\\\\ So $\bf{\lim_{y\rightarrow 0}(8+my)^{\frac{1}{3}}-n = 0\Leftrightarrow n=2}$\\\\\\ So $\bf{\lim_{y\rightarrow 0}\frac{(8+my)^{\frac{1}{3}}-2}{y}=1}$\\\\\\ $\bf{\lim_{y\rightarrow 0}\frac{2.\left(1+\frac{my}{8}\right)^{\frac{1}{3}}-2}{y}=1}$\\\\\\ $\bf{\lim_{y\rightarrow 0}\frac{\left(1+\frac{my}{8}\right)^{\frac{1}{3}}-2}{y}=\frac{1}{2}}$\\\\\\ Using expansion of $\bf{(1+x)^n}$\\\\\\ So We Get $\bf{m=12}$\\\\\\ So $\bf{m+n = 12+2=14}$
2305Ans 1-
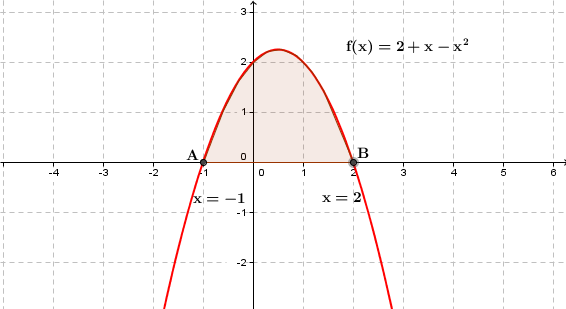
let F(x) = ∫(2+x-x2)dx
dF(x)dx = 2+x - x2
The maxima of this F(x) is obtained when 2+x-x2=0
Let a and b be the roots.
a+b = -co-efficient of xco-efficient of x2 = 1
1057