1the first limit exists ....
in fact for all a>0 in xasin(1/x) , this limit will exist
as x→0 ,1/x→∞ sa the value of sin(1/x) can be anything in [-1,1]
so as x→0 say it is 1/100000000.. ...this is just for explaining
if a is negative it will reverse i.e. will become 1000000....
so the value can be anything between -∞ to +∞ .........as the value id not fixed ..we will say that the limit does not exist .
but if a>0 then (1/1000000..)a....would certainly give zero
so the limit would be 0
1
Shriya
·2009-06-26 07:38:16
i think the same concept will apply for the second one ....the value of tan(1/x) will hover from -∞ to ∞ .....but am not sure ..
the third one is simple ...limit does not exist
1the third one is correct limit x→0 tan(1/x) wont exist
as to the others just out of curiosity I did some research, and actually got the graphs of the functions
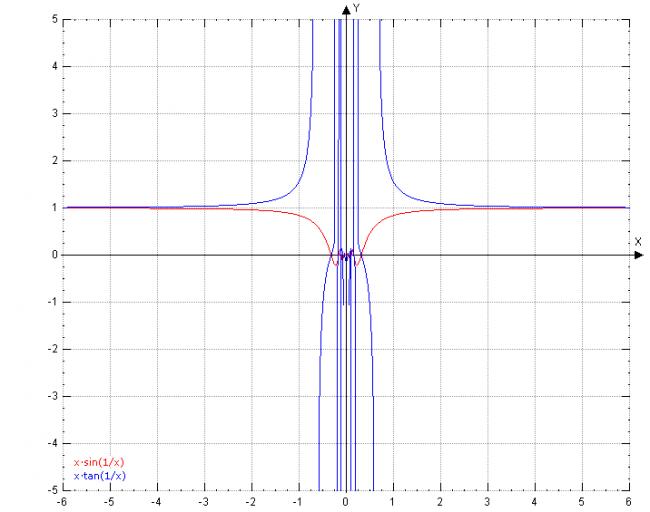
blue-x* tan (1/x)
red-x* sin(1/x)
since the red graph seems to be close to 0 , the limit is proabably 0. As for the blue graph can we conclude that the limit is ∞???
@shriya
the q is not xa sin (1/x)
it is x multiplied by sin(1/x)
and same for the second Q
1
cipher1729
·2009-06-27 19:31:08
@shriya
and yeah, thanks again
66What's going on....
the question says x tan(1/x) .... and ppl seem to be discussing x sin(1/x)
1
Shriya
·2009-06-27 20:51:56
i know that it is not xa but if we put a=1 ..your question appears
this limit will be zero for all a>0, so it is zero for a=1 also
1best thing is 2 apply corollary of sandwich thm
u get answer for limx -->0 x *tan(1/x) as 0 staright away
