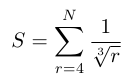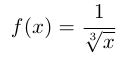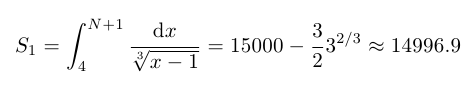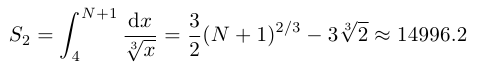Sum

please please suggest a method to solve these type of questions.

How to solve? i am not getting any hint. i Don't have any experience to solve this type of questions.

Let N = 10⁶. Then the given sum
S = \sum_{r=4}^N \dfrac{1}{\sqrt[3]{r}}
Consider the function
f(x) = \dfrac{1}{\sqrt[3]{x}}
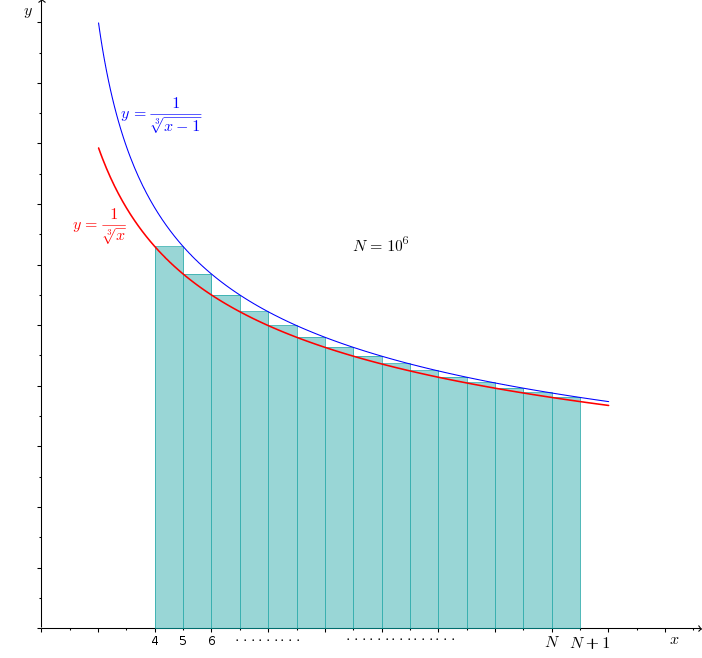
We notice that each term of the given sum are simply f(4), f(5), . . ., f(N). Geometrically, we can interpret S as the sum of the areas of rectangles having its height as f(4), f(5), ... while the width is 1 for all of them. This has been shown by the greenish shaded portion in the following diagram:

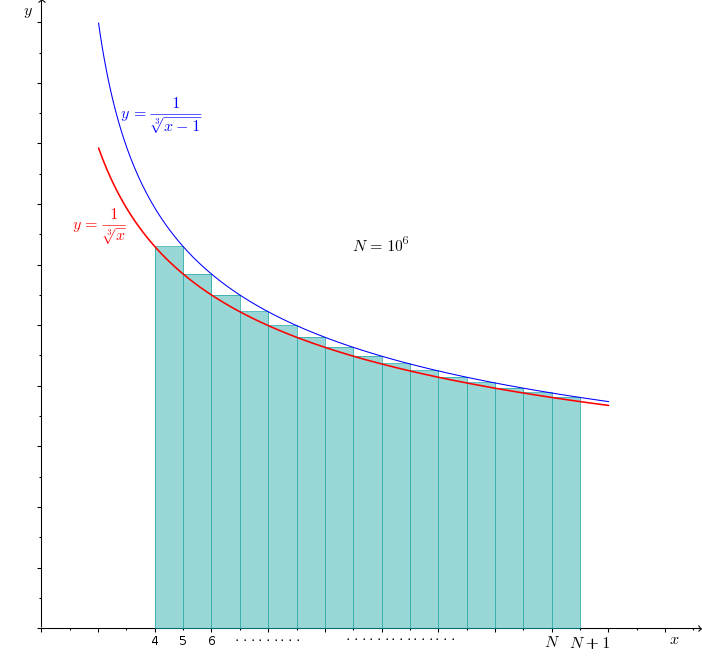
You can easily see that S is bounded by the areas
S_1=\int_4^{N+1} \dfrac{\mathrm{d}x}{\sqrt[3]{x-1}}\approx 14996.9
from above and by
S_2=\int_4^{N+1} \dfrac{\mathrm{d}x}{\sqrt[3]{x}}\approx 14996.2
from below. Hence
14996.2 < S < 14996.9
Therefore, [S]= 14996