24no one !!!!!
I read this question somewhere and thought it was a good one......posting here to test eveyone's intelligence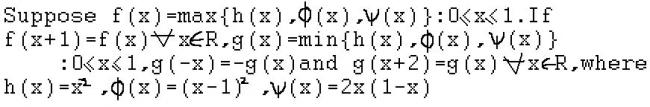
-
UP 0 DOWN 0 0 11
11 Answers
1the first one simlifies to =
3∫f(x)dx
= 3(0∫1/3(x-1)2dx+1/3∫2/32x(1-x)dx+2/3∫1x2dx
1for (2)
min value of f(x) comes out to be 4/9
max value of g(x) comes out to be 1/4
1for (3)
it is nothing but
0∫1g(x)dx
which is equal to
0∫1/2x2dx+1/2∫1(x-1)2dx
i think thre is some thing wrong with your picture rohan.1oops i didnt analyze g(x) properly ,
now i have got it and corrected it
i was doing without a pen to draw
i should have drawn a rough sketch !!
1for part 4
from the graph we can see that f(x)
lies above g(x) in both (-1,0) and (0,1)
and we can figure out that if the point of non differentiability of g(x) is made to go 1/4 units upward
it will cut f(x) at exactly one point