For the solution to the first sum...
how cud the numerator of |2x-1/x-1| become = 2+1 ???????????????????????????????
Ok here r a few ques i found quite tricky...well at least to me they were tricky..and hence i cud not solve them:)so pls do me a favour and solve them for me.
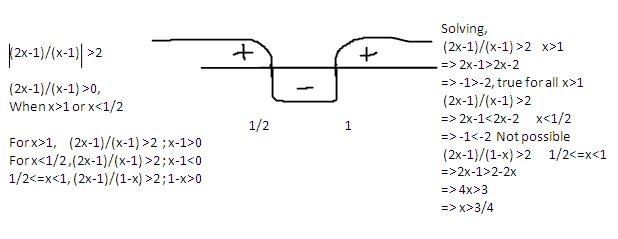
1)Solve |2x-1/x-1|>2
2)Solve |x/x-1|+|x|=x2/|x-1|
3)solve (x+3)5 - (x-1)5 ≥ 244
4)Prove that for all real x,y the value of x2+2xy+3y2-6x-2y cannot be less than -11
-
UP 0 DOWN 0 0 8

8 Answers
|2x-1/x-1|>2
= |2+1/(x-1)| > 2
THus, 1/(x-1)>0 or 1/(x-1) < -4
now solve this one
|x/x-1|+|x|=x2/|x-1|
|x|{1/|x-1|+1} = x2/|x-1|
Thus,
{1/|x-1|+1} = |x|/|x-1|
1+|x-1| = |x|
1 = |x|-|x-1|
thus, x>=1 is the solution....
(x+3)5 - (x-1)5 ≥ 244
lets take some integers and try to figure for which integer x, the equality holds!
3^5 = 243 and (-1)^5 = -1
thus x=0 seems to be a solution to the equality.
Now, can you try?
f(x)=(x+3)5-(x-1)5-244.....f'(x)=10(2x+2).k......where k>0 for all x....
f'(x)>0 for all x>-2....
f(0)=0, thus for all positive x the above inequality holds.....[33]
x2+2xy+3y2-6x-2y
(x+y)2+2y2-6x-2y
now look at (x+y)2.. can we add another constant to this and get a perfect square....
(x+y)2+2y2-6(x+y)+4y
(x+y)2-6(x+y)+2y2+4y
(x+y)2-6(x+y)+9+2y2+4y+2-11
(x+y-3)2+2(y+1)2 -11
Hence proved the last one :)