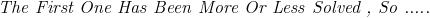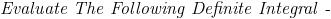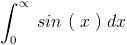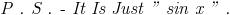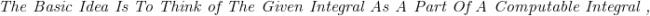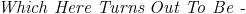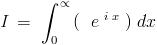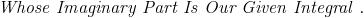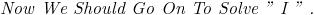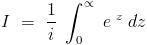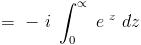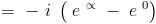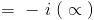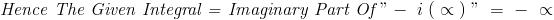39is it just sin x ??
13 Answers
62Bhargav.. are you kidding :P This is a definite integral ;)
And we have this one as one which is much easier googlable than the previous question where you commented the same ;)
39oh!
my bad!!
i try googling something only when i utterly fail at it :D
341That's a strange result. f(t) = \int_0^t \sin x \ dx is a continuous function.
Now consider the sequence a_n = 4n \pi and the induced sequence b_n = f(a_n)
By continuity, \lim_{n \rightarrow \infty} b_n = f\left(\lim_{n \rightarrow \infty} a_n \right). LHS is obviously zero.
Now we consider another sequence a_n = \dfrac{(4n+1)\pi}{2} and the induced sequence defined as above and you get LHS=1.
So we have a contradiction right?
62it is strange because gallardo forgot to change the limit of the integral at one stage...
And anyway we know that this is not a convergent sequence... and the value fluctuates with a minimum of zero to a maximum of 2...
341Precisely, the max is 2. So the lim cannot be infinity. Further, the limit itself does not exist.
I dont rmmbr much of complex variable integration, but you've got to specify a path over which the integral is calculated.
62yup.. and the problem is when there are points where the functino is not defined.. had studied in my 1st year.. dont remember much either ;)
btw this is a question which is equivalent to the famous sum or the fallacy which is
1-1+1-1+1..... infinity...
The integral here is the continuous counterpart of the discrete sum.....
66arihant books, as usual, are not by persons who are masters of their fields. And personally, I always disprove of these books.
1see
post no ( # 6 )
WONDERFUL PROOF BY BIPIN DUBEY SIR......
http://www.targetiit.com/iit-jee-forum/posts/integrate-it-14647.html
66@soumikamandal,
That proof is not correct. The result is
\int_0^\infty e^{-ax}\sin x\ \mathrm dx =\dfrac{1}{1+a^2}\qquad (\mathbf{a>0})
The last part (in bold) is necessary for the convergence of the given integral. (Basically, the above result is something called the Laplace transform of sin x). And if you put a=0, the condition a>0 is definitely not true.