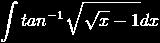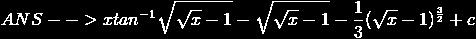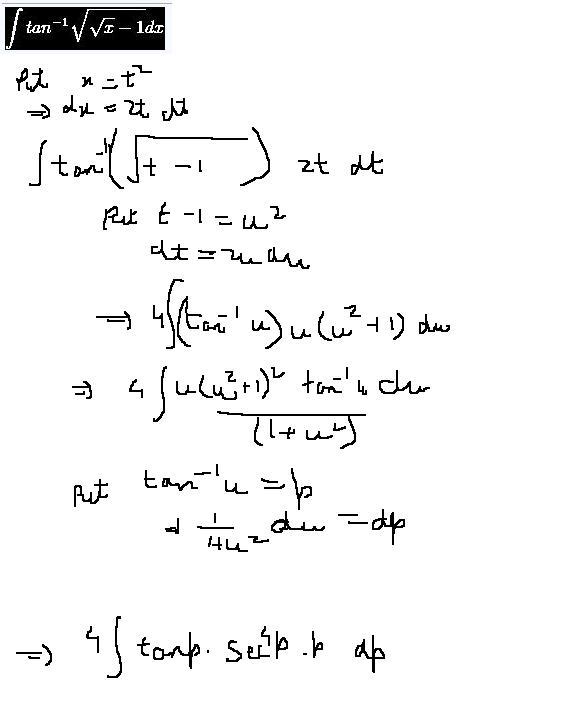TOUGH INTEGRAL(1)

yes u can use by -parts or trigonometric substitution

i was trying in a diff way and got stuck...can anyone help ???

let

x = sec ^4 \theta

dx = 4 sec^3 \theta .sec \theta .tan \theta

dx = 4 sec^4 \theta .tan \theta

integral reduces to

\int \tan^{-1} \sqrt{ \sqrt{sec ^4 \theta }-1}

\int \tan^{-1} \sqrt{ {sec ^2 \theta }-1}

\int \tan^{-1} \sqrt{ {tan ^2 \theta }}

forgot to write dx in all above steps
so writing below from now onwards

\int \tan^{-1} \sqrt{ {tan ^2 \theta }} dx

\int \theta .4sec^4 \theta. tan\theta . d\theta

\int \theta .4sec^3 \theta. sec\theta . tan\theta . d\theta

put

sec\theta = t

sec\theta . tan\theta d\theta = dt

integral reduces to

4 \int \theta . t^3 dt .

4 \int sec ^{-1} t . t^3 dt .

= 4 I

now using by parts I =

sec^{-1}t \int t^3 - \int \left(\frac{1}{( t ) ( \sqrt{t^2-1 }} \right) .\int t^3

sec^{-1}t .\frac{t^4}{4} - \frac{1}{4}\int \frac{t^3}{\sqrt{t^2-1 }}.dt

sec^{-1}t .\frac{t^4}{4} - \frac{1}{4}\int \frac{t^2 . t }{\sqrt{t^2-1 }}.dt

put t² - 1 = u ( → t² = u + 1 )

2t dt = du

t dt =du2

integral reduces as

sec^{-1}t .\frac{t^4}{4} - \frac{1}{8}\int \frac{ u + 1 }{\sqrt{u }}.dt

sec^{-1}t .\frac{t^4}{4} - \frac{1}{8}\left( \int \sqrt{u } . du + \int \frac{1.du }{\sqrt{u}}\right)

sec^{-1}t .\frac{t^4}{4} - \frac{1}{8}\left( \frac{2}{3}( u)^{\frac{3}{2}} + 2\sqrt{u}\right)

sec^{-1}t .\frac{t^4}{4} - \frac{u ^{\frac{3}{2}}}{4. 3} -\frac{\sqrt{u}}{4}

therefore

4 I =

sec^{-1}t . t^4 - \frac{( t ^2 - 1 ) ^{\frac{3}{2}}}{ 3} -\sqrt{t^ 2- 1}

sec ^ 4\theta = x

1 + tan ^ 2\theta = \sqrt{x}

tan ^ 2\theta = \sqrt{x} - 1

tan \theta = \sqrt{\sqrt{x} - 1}

\theta = \tan^{-1} ( \sqrt{\sqrt{x} - 1} )

t^ 4 = sec^4 \theta = x

t^ 2 - 1 = sec^ 2 \theta - 1 = \sqrt{x} - 1

combining all

finally integral reduces to __

\tan^{-1} \sqrt{\sqrt{x}- 1} . x - \frac{(\sqrt{x}-1 ) ^{\frac{3}{2}}}{3} - \sqrt{\sqrt{x}- 1} + c

@ eureka

write sec ⁴ θtan θ

as sec ³Î¸ sec θtan θ

and then put sec θ = t then ur done

btw mine and ur solution are one and same see mine ..

for θ integ by parts

but there is one θ too there...