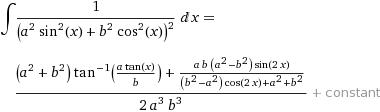arrey aishwarya u r gettin an ans atleast m nd stuck up hw to break it......
18 Answers
TAPAS YAAR MUJHE YE
" WOLFRAM MATHEMATICA " WAALA ANSWER NAHI CHAHIYE !
yes bhaiya
i just wanted to write
some constant k such that
kt=z
actually i didnt mean the previous constant k (soryy for dat )
i think you should use the substitution √k t = z
Otherwise it seems fine.. [1]
not quite sure
done it roughly
\int \frac{(1+\tan^2x)\sec^2dx}{\left(a^2\tan^2x+b^2 \right)^2} \\ \\ put \ tanx =t \\ \int \frac{\left( 1+t^2\right).dt}{\left( kt^2 +1\right)^2 }\\ \int \frac{dt}{\left( kt^2 +1\right)^2} +\int \frac{t^2.dt}{\left( kt^2 +1\right)^2}\\ put \ k_2t=z \\ such \ that \ the \ integral \ becomes \\ \int k_1\frac{dz}{\left( z^2 +1\right)^2} + k_2\int \frac{z^2.dz}{\left( z^2 +1\right)^2}\\ now \ put \ z=\tan\alpha \\ k_1\int \cos^2\alpha + k_2\int \sin^2 \alpha
All right the correct answer is complicated as well.
http://www.wolframalpha.com/input/?i=integrate+1%2F%28%28a^2+%28sin+x%29^2+%2B+b^2%28cosx%29^2%29%29^2+dx+
but yea ..it is integrable
plz answer ------ is it integrable or not integrable -------------
arrey wahi toh comedy hai..i jst got condused...lol..
oh god i was goiin to apply chain rule by mistake.dats y i got sum rong ans.......