Can someone help....!

well it can be proved with help of calculus.
see some posts here
http://in.answers.yahoo.com/question/index?qid=20091227052735AAbTTa2

here it goes

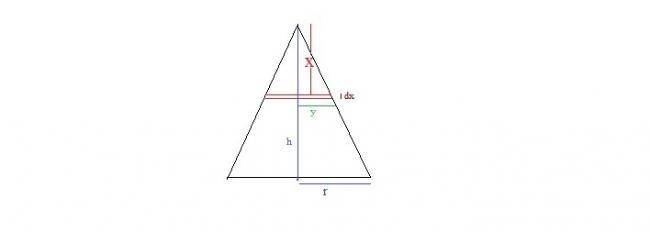
first think about the shape of a cone.

isn't it like vertically gathering some cylinder of negligible height and decreasing radius?
so we will try to find volume of these cylinders and then sum it up

let us choose a cylinder of height dx(very small) which is at a distance x from the top of the cone.(see figure)

let y be the radius of the cylinder .

so we have x/y = h/r

or, y= xr/h

now we can surely find the volume of that cylinder,let us call it dV(very small)

so dV= \Pi y^2 dx \Rightarrow dV= \Pi (x^2r^2/h^2)dx

as you can see if x ranges from 0 to h(height of the cylinder) we can cover the whole cone or say we can make a cone

so if we are to find the volume of the cone we will just integrate with lower limit 0 and upper limit h

so volume of the cone v = ∫dv = \int_{0}^{h}{} \Pi (x^2 r^2 /h^2)dx = \Pi ( r^2/h^2) \int_{0}^{h}{} x^2 dx = 1/3 \Pi r^2 h

note that \int_{0}^{h}{} x^2dx = h^3/3

@shubho

Thanks a lot dear....!