6)every odd number is of the form (2n+1)
now (2n+1)2 = 4n2 + 4n +1
=4n(n+1) +1
=8k +1 [as, n(n+1) is divisible by 2!]
Kya aap tenth pass se tej hein? .
Are u smarter than a tenth grade? check out.............!!!!!!
Solve these easy tenth level questions. for everyone.....
1. If triangles ABC and ABM are similar then LA + LD = ?
2. The sum of the squares of the medians of a triangle is (45 + 3/4) cm2.
The product of all the three respective sides are 72 cm3. If one of the
sides of a triangle is 3 cm. Then, find all the sides of the triangle.
3. Prove that the area of a sector is ∠r2ѳ/360° and the length of the
arc is [2âˆrѳ/360° - r2/2 sinѳ].
4. Prove that sec ѳ > 1, ѳ lies between 0 and pi/2
5. Prove that the sum of the squares of the sides of a parallelogram is equal to
the sum of the squares of its corresponding diagonals.
6. Show that for odd positive integer to be a perfect square, it should be of the form 8k + 1
7. Prove that 400289158 can be written as the sum of two squares.
8. Prove that a0 = 1
9. Prove that 1n + 8n - 6n - 3n is divisible by 10.
10. Prove that tangent to the circle at a point is perpendicular to the radius
of the circle through that point.
11. 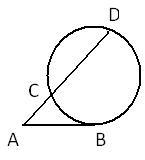
AB is the tangent to the circle at point B. Prove that AB2 = AC x AD
-
UP 0 DOWN 0 0 14

14 Answers
Actually not sir!
Neither i hv posted this to check some one
It will simply help me boost up my problem solving skills
But How? -> I'll post it later on. [well know the solution to each and every problem]
posted above..
11th is based on angles in alternate segments ( theorem in 10th std)
10th can be proved by assuming the opposite, and reaching a contradiction
i didnot undestand 1st one
1. Actually the first question is wrong.... don't feel bad over this please
11th will be proved by similarity if we join B with C and B with D
Then triangle BAC will be similar to triangle DAB [by AA criterion]
and so on............
But no one gave a try to Questions 2, 5, 7, 9
9) its easy..write it as 8n-3n -(6n-1n) thus a multiple of 5
and 8n-6n-(3n-1n) multiple of 2
so divisible by 10
5)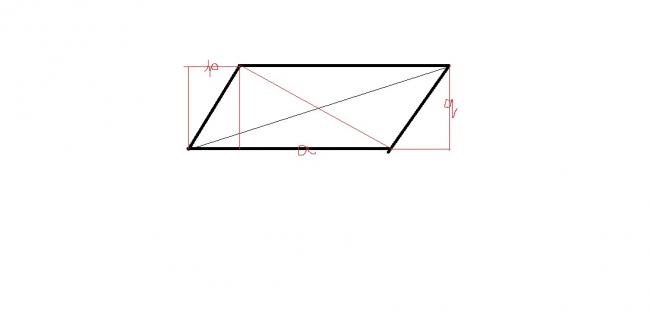
sum of squares of sides = 2(q2+p2) + 2a2
sum of squares of diagonals =(a-p)2 + (a+p)2 + 2q2
(ri8 angled triangles)
What have you done in question 5?.......
Solve it by plane geometry.....
ur solution is not at all clr.....!
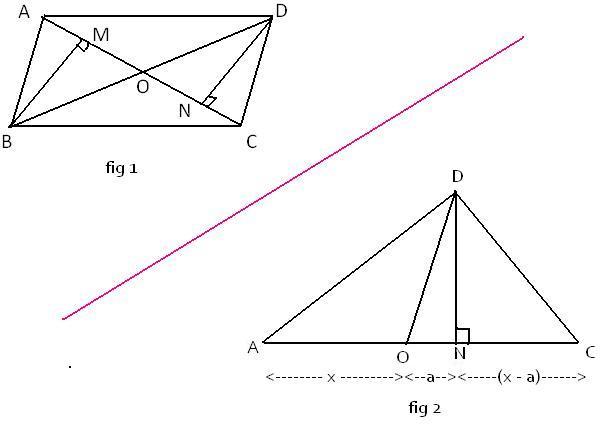
Given : ||gm ABCD with diagonals AC and BD intersecting at O
Construction : We drop perpendiculars BM and DN from B and D and finally
triangle ADC can be represendted in the fig 2 clearly.
proof : Using pythagora's theorem,
AD2 + CD2 = 2DN2 + AN2 + CN2 = 2DN2 + (x + a)2 + (x - a)2
= 2 (DN2 + x2 + a2) = 2 (x2 + OD2)
but, x = OA = AC/2 and OD = BD/2
Thus, AD2 + CD2 = 2 (AC2 + BD2/4) = [AC2 + BD2]/2 ------------ (i)
similarly in triangle ABC we get,
AB2 + BC2 = [AC2 + BD2]/2 ------------------- (ii)
Adding eqns. (i) and (ii) we get....
AB2 + BC2 + CD2 + AD2 = AC2 + BD2 proved.......
This is based on the fact that if a number on division by 4 leaves remainder 0,1 or 2
then it can be written as the sum of two squares or else not...
proof for this fact or theorem.....
any integer is either of the form 2k or 2k+1
Now, there are three cases:
Remainder when 4 divides the sum of the squares of
1. Two even integers.
2. One even and one odd integer.
3. Two odd integers.
Let's check out....
for the first case...
(2k)2 + (2k)2 = 8k2 -> remainder = 0 [when divided by 4]
for the second case
(2k)2 + (2k + 1)2 = 4k2 + 4k2 + 4k + 1 = 8k2 + 4k + 1 -> remainder = 1 [when divided by 4]
for the third case
(2k + 1)2 + (2k + 1)2 = 2(4k2 + 4k + 1) = 8k2 + 8k + 2 -> remainder = 2 [when divided by 4]
So we conclude that the sum of the squares of two positive integers leaves remainder 0,1 or 2 when divided by 4
Now on dividing 400289158 by 4 we get the remainder to be 2
and so it can be written as the sum of two squares proved....
wasn't that cool..............
tha wasn't enough clr....k...!
u didn't show the methods.....
and no one can make that out simply by seeing your figure......!