Let a ΔABC with <BAC=60°. Bisectors of angles <ABC and <ACB be BE and CF respectively.
Let BE and CF intersect at I(Incentre).
So, we get <BIC=90°+1/2(<BAC)
=120°
So, <BIC=2<BAC.
Therefore I is the Circumcentre of ΔABC as well.
→BI=CI
→<IBC=<ICB
→<IBC=30°
→<ABC=<ACB=60°
Please show me where I am wrong.
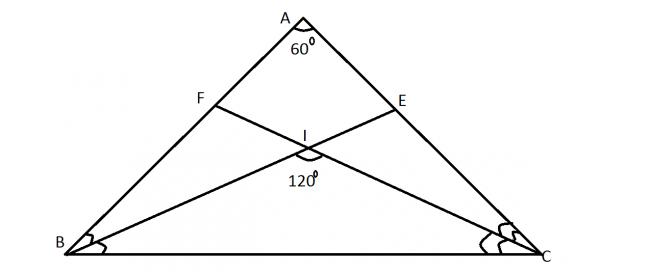
1If\angle BIC =2 \angle BAC
that doesnt mean that I is always the circumcentre.
Lets suppose in your figure only (PLEASE SUPPOSE)
that \Delta BEC is equilateral with \angle BIC = 120^{\circ}.Then by your explanation I is the circumcentre of the equilateral triangle \Delta BEC which is not possible
:)
11According to me the assumption of I as the circumcentre is wrong.
21Thank you @ninepiontcircle as well as @Sambit.
I understood it now.
